题目内容
已知不重合的两直线 与
与 对应的斜率分别为
对应的斜率分别为 与
与 ,则“
,则“ ”是“
”是“ ∥
∥ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不是充分也不是必要条件 |
A
解析试题分析:前提是两条不重合的直线,所以当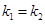 时,有
时,有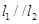 ,但当
,但当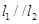 时,却得不到
时,却得不到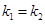 ,因为当两条直线平行但斜率不存在时,谈不上斜率的问题,如直线
,因为当两条直线平行但斜率不存在时,谈不上斜率的问题,如直线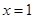 与直线
与直线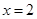 平行,却得不出直线的斜率,故“
平行,却得不出直线的斜率,故“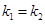 ”是“
”是“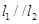 ”的充分不必要条件,选A.
”的充分不必要条件,选A.
考点:1.充分必要条件;2.两直线平行的条件.

练习册系列答案
相关题目
“ ”是“
”是“ ”的
”的
| A.必要不充分条件 | B.充分不必要条件 |
| C.充要条件 | D.既不充分也不必要条件 |
命题“ ”的否定是( )
”的否定是( )
A. | B. |
C. | D. |
命题“若 ,则
,则 是直角三角形”的逆命题、否命题、逆否命题这三个命题中,真命题的个数是( )
是直角三角形”的逆命题、否命题、逆否命题这三个命题中,真命题的个数是( )
| A.0 | B.1 | C.2 | D.3 |
设 ,
,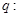 关于
关于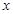 的方程
的方程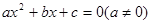 有实根,则
有实根,则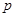 是
是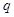 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知a>0,函数f(x)=ax2+bx+c,若x0满足关于x的方程2ax+b=0,则下列选项的命题中为假命题的是( )
| A.?x∈R,f(x)≤f(x0) | B.?x∈R,f(x)≥f(x0) |
| C.?x∈R,f(x)≤f(x0) | D.?x∈R,f(x)≥f(x0) |
下列说法中,不正确的是( )
A.命题p:?x∈R,sinx≤1,则 p:?x∈R,sinx>1 p:?x∈R,sinx>1 |
B.在△ABC中,“A>30°”是“sinA> ”的必要不充分条件 ”的必要不充分条件 |
C.命题p:点( ,0)为函数f(x)=tan(2x+ ,0)为函数f(x)=tan(2x+ )的一个对称中心;命题q:如果|a|=1,|b|=2,<a,b>=120°,那么b在a方向上的投影为1,则( )的一个对称中心;命题q:如果|a|=1,|b|=2,<a,b>=120°,那么b在a方向上的投影为1,则( p)∨( p)∨( q)为真命题 q)为真命题 |
| D.命题“在△ABC中,若sinA=sinB,则△ABC为等腰三角形”的否命题为真命题 |
下列命题中是真命题的是( )
A. x∈R,使得sinxcosx= x∈R,使得sinxcosx= |
B. x∈(-∞,0),2x>1 x∈(-∞,0),2x>1 |
C. x∈R,x2≥x+1 x∈R,x2≥x+1 |
D. x∈(0, x∈(0, ),tanx>sinx ),tanx>sinx |