题目内容
已知等比数列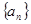 各项均为正数,前
各项均为正数,前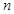 项和为
项和为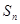 ,若
,若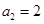 ,
,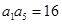 .则公比q= ,
.则公比q= ,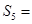 .
.
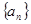 各项均为正数,前
各项均为正数,前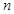 项和为
项和为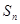 ,若
,若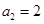 ,
,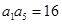 .则公比q= ,
.则公比q= ,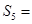 .
. 2, 31.
试题分析: 因为等比数列的各项都是正数,且
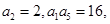 设其公比为q,那么可知
设其公比为q,那么可知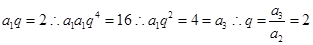 ,故可知公比为2,首项为1,那么
,故可知公比为2,首项为1,那么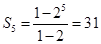 ,因此答案为2,31.
,因此答案为2,31.点评:解决该试题的关键是根据数列的前几项的关系式,联立方程组得到公比和首项的值,得到解决。

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
题目内容
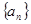 各项均为正数,前
各项均为正数,前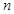 项和为
项和为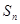 ,若
,若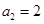 ,
,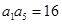 .则公比q= ,
.则公比q= ,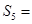 .
. 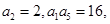 设其公比为q,那么可知
设其公比为q,那么可知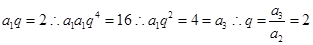 ,故可知公比为2,首项为1,那么
,故可知公比为2,首项为1,那么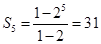 ,因此答案为2,31.
,因此答案为2,31.
 名校通行证有效作业系列答案
名校通行证有效作业系列答案