题目内容
在等比数列{an}中,a1+a2+…+an=2n-1(n∈N*),则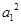 +
+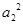 +…+
+…+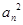 等于( )
等于( )
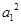 +
+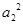 +…+
+…+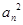 等于( )
等于( )| A.(2n-1)2 | B.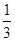 (2n-1)2 (2n-1)2 | C.4n-1 | D.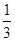 (4n-1) (4n-1) |
D
因为在等比数列{an}中,a1+a2+…+an=2n-1(n∈N*),则可知原数列的公比为2,首项为1,那么所求的数列的公比为4,首项为1,因此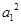 +
+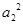 +…+
+…+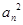 等于
等于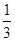 (4n-1),选D
(4n-1),选D
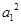 +
+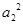 +…+
+…+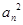 等于
等于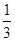 (4n-1),选D
(4n-1),选D
练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
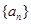 中,
中,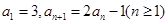
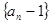 是等比数列;
是等比数列;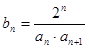 ,求证:数列
,求证:数列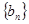 的前
的前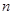 项和
项和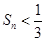 .
.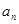 与
与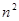 的大小(
的大小(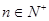 )。
)。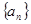 各项均为正数,前
各项均为正数,前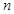 项和为
项和为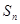 ,若
,若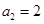 ,
,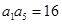 .则公比q= ,
.则公比q= ,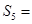 .
. 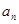 }中,
}中,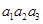 =5,
=5,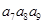 =10,则
=10,则
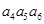 =( )
=( )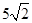
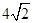
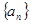 中,
中,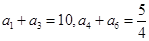 ,求
,求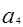 及其前5项的和
及其前5项的和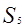 .
.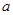 ,
,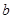 ,
,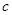 成等比数列,其公比为3,如果
成等比数列,其公比为3,如果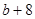 ,
, 成等差数列,求这三个数.
成等差数列,求这三个数. 是等比数列,
是等比数列,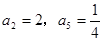 ,则
,则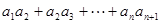 =( )
=( )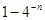 )
) 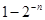 )
)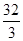 (
(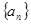 为等比数列,且
为等比数列,且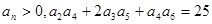 ,则
,则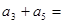 ( )
( )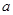 n}的各项均为正数,公比q≠1,设P=
n}的各项均为正数,公比q≠1,设P=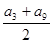 ,Q=
,Q=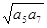 则P与Q的大小关系是( )
则P与Q的大小关系是( )