题目内容
14.把复数z的共轭复数记作$\overline{z}$,i是虚数单位,已知(1+2i)$\overline{z}$=4+3i.(1)求z;
(2)求$\frac{z}{\overline{z}}$.
分析 利用已知求出$\overline{z}$,再求z,并且进行运算.
解答 解:因为(1+2i)$\overline{z}$=4+3i.
所以$\overline{z}=\frac{4+3i}{1+2i}=\frac{(4+3i)(1-2i)}{(1+2i)(1-2i)}$=$\frac{10-5i}{5}$=2-i;
所以(1)z=2+i;
(2)$\frac{z}{\overline{z}}$=$\frac{2+i}{2-i}=\frac{(2+i)(2+i)}{(2-i)(2+i)}=\frac{3+4i}{5}=\frac{3}{5}+\frac{4}{5}i$.
点评 本题考查了复数的除法运算;一般的将分子、分母乘分母的共轭复数,使分母实数化.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
4.满足条件|z-i|=|z+3+4i|的复数z在复平面内对应的点的轨迹是( )
| A. | 一条直线 | B. | 两条直线 | C. | 圆 | D. | 椭圆 |
9.复数m2+2m-3+(m-1)i(m∈R)为纯虚数,则( )
| A. | m=1,m=-3 | B. | m=1 | C. | m=-3 | D. | m=3 |
 函数y=tan($\frac{π}{4}$x-$\frac{π}{2}$)(0<x<4)的图象如图所示,A为图象与x轴的交点,过点A的直线l与函数的图象交于B、C两点,则($\overrightarrow{OB}$+$\overrightarrow{OC}$)•$\overrightarrow{OA}$等于( )
函数y=tan($\frac{π}{4}$x-$\frac{π}{2}$)(0<x<4)的图象如图所示,A为图象与x轴的交点,过点A的直线l与函数的图象交于B、C两点,则($\overrightarrow{OB}$+$\overrightarrow{OC}$)•$\overrightarrow{OA}$等于( )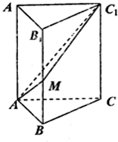 如图,直三棱柱ABCD-A1B1C1中,AB=1,BC=2,AC=$\sqrt{5}$,AA1=3,M为线段BB1上的一动点,则当AM+MC1最小时,点C到平面AMC1的距离为$\sqrt{3}$.
如图,直三棱柱ABCD-A1B1C1中,AB=1,BC=2,AC=$\sqrt{5}$,AA1=3,M为线段BB1上的一动点,则当AM+MC1最小时,点C到平面AMC1的距离为$\sqrt{3}$.