Question

【题目】已知函数，不等式对恒成立．

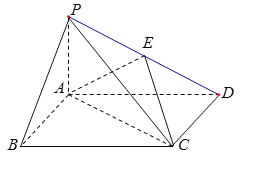
（1）求函数的极值和函数的图象在点处的切线方程；

（2）求实数的取值的集合；

（3）设，函数，，其中为自然对数的底数，若关于的不等式至少有一个解，求的取值范围．

Answer 1

【答案】（1）极大值为，无极小值； ；（2） ；（3）.

【解析】

（1）对求导，然后利用导数大于零和导数小于零，求得函数的单调区间，由此求得函数的极值.通过求出切点和斜率，利用点斜式求得切线方程.（2）当时不合题意.当时，对两边取以为底的对数，转化为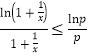对恒成立.根据（1）中函数的单调性以及极大值，可求得的值.（3）将关于的不等式左边构造为函数，对分成和两类，分别利用函数的值域，和函数的导数，求解出的取值范围.

（1），则时，时，故在递增，在递减，故； 又，故函数的图象在点处的切线方程为：

（2）显然，不合题意。当时，由得，则有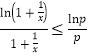，故依题意知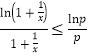对恒成立.由前面的结论知，当时，取得最大值，故.又可知，当时，取得最大值，故 .故，综上得 .

（3）设则.当时，，所以不存在 使得成立．故不合题意.当时，.因为， 所以在恒成立，故在单调递减，，则依题意有.解之得故的取值范围