Question

7．已知函数f（x）=|x|（x-a），a∈R．
（1）讨论f（x）在R上的奇偶性；
（2当a≤0时，求函数f（x）在闭区间[-1，$\frac{1}{2}$]上的最大值．

Answer 1

分析 （1）对a分a=0与a≠0两类讨论，利用函数奇偶性的定义判断即可；
（2）讨论a的取值范围，结合一元二次函数的单调性的性质即可得到结论．

解答 解：（1）当a=0时，f（x）=|x|x，f（-x）=-f（x），即f（x）是奇函数；
当a≠0时，f（-x）≠f（x），且f（-x）≠-f（x），
此时f（x）既不是奇函数也不是偶函数．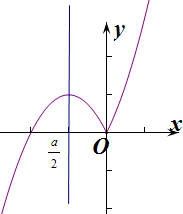
（2）若a=0，则f（x）=|x|x=$\left\{\begin{array}{l}{{x}^{2}，}&{x≥0}\\{-{x}^{2}，}&{x＜0}\end{array}\right.$，
则函数f（x）在R上为增函数，
则在闭区间[-1，$\frac{1}{2}$]上的最大值为f（$\frac{1}{2}$）=$\frac{1}{4}$．
若a＜0，则当x＞0时，f（x）=x（x-a）为增函数，
当x≤0时，f（x）=-x（x-a）=-（x-$\frac{a}{2}$）²+$\frac{{a}^{2}}{4}$，
此时对称轴为x=$\frac{a}{2}$．
f（$\frac{1}{2}$）=$\frac{1-2a}{4}$，
①若$\frac{a}{2}$≤-1，即a≤-2，
此时函数在[-1，0]上递减，
f（-1）=-1-a，
f（$\frac{1}{2}$）-f（-1）=$\frac{1-2a}{4}$+1+a=$\frac{2a+5}{2}$，
若f（$\frac{1}{2}$）-f（-1）≥0，解得a≥-$\frac{5}{2}$，此时f（$\frac{1}{2}$）≥f（1），
即当-$\frac{5}{2}$≤a≤-2时，函数在闭区间[-1，$\frac{1}{2}$]上的最大值为f（$\frac{1}{2}$）=$\frac{1-2a}{4}$．
若f（$\frac{1}{2}$）-f（-1）＜0，解得a＜-$\frac{5}{2}$，此时f（$\frac{1}{2}$）＜f（-1），
即当a＜-$\frac{5}{2}$时，函数在闭区间[-1，$\frac{1}{2}$]上的最大值为f（-1）=-1-a．
②若-1＜$\frac{a}{2}$＜0，即-2＜a＜0，
f（$\frac{a}{2}$）=$\frac{{a}^{2}}{4}$，f（$\frac{1}{2}$）=$\frac{1-2a}{4}$．
则f（$\frac{a}{2}$）-f（$\frac{1}{2}$）=$\frac{{a}^{2}}{4}$-$\frac{1-2a}{4}$=$\frac{{a}^{2}+2a-1}{4}$．
若f（$\frac{a}{2}$）-f（$\frac{1}{2}$）=$\frac{{a}^{2}+2a-1}{4}$≥0，解得a≤-1-$\sqrt{2}$，即此时不等式无解，
若f（$\frac{a}{2}$）-f（$\frac{1}{2}$）=$\frac{{a}^{2}+2a-1}{4}$＜0，解得-1-$\sqrt{2}$＜a＜0，即-2＜a＜0，此时f（$\frac{a}{2}$）＜f（$\frac{1}{2}$），
即当-2＜a＜0时，函数在闭区间[-1，$\frac{1}{2}$]上的最大值为f（$\frac{1}{2}$）=$\frac{1-2a}{4}$．

点评 本题考查带绝对值的函数，考查二次函数及其最值，考查作图能力，分析问题，解决问题的能力，考查分类讨论思想，属于难题．