Question

（13分）（2011•广东）如图所示的几何体是将高为2，底面半径为1的直圆柱沿过轴的平面切开后，将其中一半沿切面向右水平平移后得到的，A，A′，B，B′分别为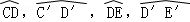的中点，O₁，O₁′，O₂，O₂′分别为CD，C′D′，DE，D′E′的中点．

（1）证明：O₁′，A′，O₂，B四点共面；
（2）设G为A A′中点，延长A′O₁′到H′，使得O₁′H′=A′O₁′．证明：BO₂′⊥平面H′B′G

Answer 1

（1）（2）见解析

解析试题分析：（1）要证O₁′，A′，O₂，B四点共面，即可证四边形BO₂A^′O₁^′为平面图形，根据A′O₁′与B′O₂′在未平移时属于同一条直径
知道A^′O₁^′∥B^′O₂^′即BO₂∥A^′O₁^′再根据BO₂=A′O₁′=1即可得到四边形BO₂A^′O₁^′是平行四边形，则证．
（2）建立空间直角坐标系，要证BO₂′⊥平面H′B′G只需证，，根据坐标运算算出•，的值均为0即可
证明：（1）∵B′，B分别是中点
∴BO₂∥B^′O₂^′
∵^{A′O1′与B′O2′}在未平移时属于同一条直径
∴A^′O₁^′∥B^′O₂^′
∴BO₂∥A^′O₁^′
∵BO₂=A′O₁′=1
∴四边形BO₂A^′O₁^′是平行四边形
即O₁′，A′，O₂，B四点共面
（2）以D为原点，以向量DE所在的直线为X轴，以向量DD′所在的直线为Z轴，建立如图空间直角坐标系，
则B（1，1，0），O₂′（0，1，2），H′（1，﹣1，2），A（﹣1，﹣1，0），G（﹣1，﹣1，1），B′（1，1，2）
则=（﹣1，0，2），=（﹣2，﹣2，﹣1），=（0，﹣2，0）
∵•=0，=0
∴BO₂′⊥B′G，BO₂′⊥B′H′
即，
∵B′H′∩B′G=B′，B′H′、B′G?面H′GB′
∴BO₂′⊥平面H′B′G

点评：本题考查了直线与平面垂直的判定，棱柱的结构特征，平面的基本性质及推论以及空间向量的基本知识，属于中档题．