题目内容
【题目】正整数数列![]() 满足:
满足:![]() ,
,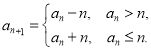
(1)写出数列![]() 的前5项;
的前5项;
(2)将数列![]() 中所有值为1的项的项数按从小到大的顺序依次排列,得到数列
中所有值为1的项的项数按从小到大的顺序依次排列,得到数列![]() ,试用
,试用![]() 表示
表示![]() (不必证明);
(不必证明);
(3)求最小的正整数![]() ,使
,使![]() .
.
【答案】(1)前五项为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据递推关系令![]() 依次求出前五项;
依次求出前五项;
(2)依次写出部分项,观察规律归纳结果,加以分析其正确性;
(3)根据(2)的结论求出![]() ,再把
,再把![]() 转化为
转化为![]() 进行分类讨论,验证其与2013的大小关系,直到
进行分类讨论,验证其与2013的大小关系,直到![]() 求解得出出具体值.
求解得出出具体值.
(1)由题:![]() ,
,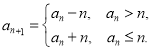 ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]()
所以前五项为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2)由题![]()
![]()
![]() ,
,
归纳![]() ,
,
显然当![]() 时,结论成立,
时,结论成立,
假设已有![]() ,显然
,显然![]() ,
,
则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
…
可以归纳:![]() ,
,
![]()
故当![]() 时,
时,![]()
因此![]() 成立;
成立;
(3)由(2)![]()
所以![]() ,
,
即![]() 是以3为首项,3为公比的等比数列,
是以3为首项,3为公比的等比数列,
![]() ,
,![]() ,
,
由![]() 可知:
可知:
当![]() 时,
时,![]() ,
,
因此当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() 或
或![]() ,即不能使
,即不能使![]() 成立,
成立,
考虑![]() 时:
时:
由(2)![]()
则![]() 解得
解得![]() ,则
,则![]() ,
,
所以![]() ,
,
所以使![]() 的最小的正整数
的最小的正整数![]() ,
,

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目