题目内容
12. 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,△PAD是等腰直角三角形,且O是斜边AD的中点,OP⊥面ABCD,AD⊥PC,PA=PC=2.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,△PAD是等腰直角三角形,且O是斜边AD的中点,OP⊥面ABCD,AD⊥PC,PA=PC=2.(Ⅰ)求证:CA=CD;
(Ⅱ)求直线PB与平面PCD所成角的正弦值.
分析 (Ⅰ)连接OP,证明OP⊥AD,然后推出AD⊥平面POC,得到AD⊥OC,证明CAD是以AD为底的等腰三角形,可得CA=CD.
(Ⅱ)以O为坐标原点,建立如图所示的空间直角坐标系O-xyz求出相关点的坐标,求出平面PCD的法向量,平面PCD的一个法向量,利用向量的数量积求解即可.
解答 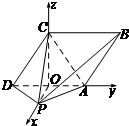 (本小题满分12分)
(本小题满分12分)
解:(Ⅰ)证明:连接OP,∵OP⊥面ABCD,
∴OP⊥AD,
又∵AD⊥PC,且OP∩CP=P,
∴AD⊥平面POC,
∴AD⊥OC,
又∵O是边AD的中点,
∴△CAD是以AD为底的等腰三角形,
∴CA=CD. …(6分)
(Ⅱ)以O为坐标原点,建立如图所示的空间直角坐标系O-xyz,$A(0,\sqrt{2},0)$,$B(0,2\sqrt{2},\sqrt{2})$,$C(0,0,\sqrt{2})$,$D(0,-\sqrt{2},0)$,$P(\sqrt{2},0,0)$,
∴$\overrightarrow{PB}=(-\sqrt{2},2\sqrt{2},\sqrt{2})$,∴$\overrightarrow{DC}=(0,\sqrt{2},\sqrt{2})$,$\overrightarrow{DP}=(\sqrt{2},\sqrt{2},0)$,…(8分)
设平面PCD的法向量为$\overrightarrow n=(x,y,z)$,
则$\left\{\begin{array}{l}\overrightarrow n•\overrightarrow{DC}=0\\ \overrightarrow n•\overrightarrow{DP}=0\end{array}\right.$,即$\left\{\begin{array}{l}0•x+\sqrt{2}y+\sqrt{2}z=0\\ \sqrt{2}x+\sqrt{2}y+0•z=0\end{array}\right.$,
即$\left\{\begin{array}{l}z=-y\\ x=-y\end{array}\right.$,不妨令y=-1,
∴平面PCD的一个法向量为$\overrightarrow n=(1,-1,1)$,…(10分)
设直线PB与平面PCD所成角为θ,
则$sinθ=|{cos<\overrightarrow n,\overrightarrow{PB}>}|=\frac{{|{\overrightarrow n•\overrightarrow{PB}}|}}{{|{\overrightarrow n}|•|{\overrightarrow{PB}}|}}$=$\frac{{2\sqrt{2}}}{{\sqrt{3}•\sqrt{12}}}=\frac{{\sqrt{2}}}{3}$.…(12分)
点评 本题考查直线与平面的垂直的判定定理的应用,直线与平面所成角的求法,考查空间想象能力以及计算能力.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案| A. | -11 | B. | 11 | C. | 31 | D. | -31 |
 甲、乙两位同学在5次考试中的数学成绩用茎叶图表示如图,中间一列的数字表示数学成绩的十位数字,两边的数字表示数学成绩的个位数字.若甲、乙两人的平均成绩分别是$\overline{{x}_{甲}}$、$\overline{{x}_{乙}}$,则下列说法正确的是( )
甲、乙两位同学在5次考试中的数学成绩用茎叶图表示如图,中间一列的数字表示数学成绩的十位数字,两边的数字表示数学成绩的个位数字.若甲、乙两人的平均成绩分别是$\overline{{x}_{甲}}$、$\overline{{x}_{乙}}$,则下列说法正确的是( )| A. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,甲比乙成绩稳定 | B. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,乙比甲成绩稳定 | ||
| C. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,甲比乙成绩稳定 | D. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,乙比甲成绩稳定 |
| A. | {0,3} | B. | {4} | C. | {0,1,2} | D. | φ |
| A. | 1+i | B. | 1-i | C. | -1-i | D. | -1+i |
 如图,在Rt△ABC中,斜边AB=5,直角边AC=4,如果以C为圆心的圆与AB相切于D,则⊙C的半径长为$\frac{12}{5}$.
如图,在Rt△ABC中,斜边AB=5,直角边AC=4,如果以C为圆心的圆与AB相切于D,则⊙C的半径长为$\frac{12}{5}$.