题目内容
已知0<a<1,试比较aa,(aa)a,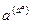 的大小.
的大小.
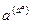 的大小.
的大小.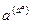 <aa<(aa)a.
<aa<(aa)a. 为比较aa与(aa)a的大小,将它们看成指数相同的两个幂.由于幂函数f(x)=xa(0<a<1=在区间[0,+∞)上是增函数,因此只需比较底数a与aa的大小.由于指数函数y=az(0<a<1=是减函数,且a<1,所以a<aa,从而aa<(aa)a.
比较aa与(aa)a的大小,也可将它们看成底数相同(都是aa)的两个幂,于是可以利用指数函数y=bx(b=aa,0<b<1)是减函数,由a<1,得到aa<(aa)a.
由于a<aa,函数y=az(0<a<1)是减函数,
因此aa>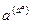 .
.
比较aa与(aa)a的大小,也可将它们看成底数相同(都是aa)的两个幂,于是可以利用指数函数y=bx(b=aa,0<b<1)是减函数,由a<1,得到aa<(aa)a.
由于a<aa,函数y=az(0<a<1)是减函数,
因此aa>
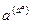 .
.
练习册系列答案
相关题目
 (m为不等于0的偶数,n为奇数,且m·n<0),那么它的大致图象是( )
(m为不等于0的偶数,n为奇数,且m·n<0),那么它的大致图象是( )

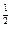 的图象经过的“卦限”是 .
的图象经过的“卦限”是 .  关于
关于 的方程
的方程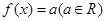 的解的个数不可能是( )
的解的个数不可能是( )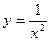
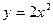
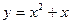
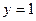
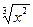 写成分数指数幂的形式为 ★
写成分数指数幂的形式为 ★ 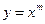 与
与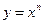 在第一象限内的图象,则( )
在第一象限内的图象,则( ) . 0<m<1
. 0<m<1 既是幂函数又是反比例函数,则这个函数是
既是幂函数又是反比例函数,则这个函数是