题目内容
若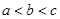 ,则函数
,则函数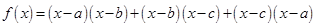 的两个零点分别位于区间( )
的两个零点分别位于区间( )
A. 和 和 内 内 |
B.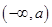 和 和 内 内 |
C. 和 和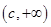 内 内 |
D.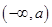 和 和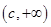 内 内 |
A
解析试题分析:∵a<b<c,∴f(a)=(a-b)(a-c)>0,f(b)=(b-c)(b-a)<0,
f(c)=(c-a)(c-b)>0,
由函数零点存在判定定理可知:在区间(a,b),(b,c)内分别存在一个零点;
又函数f(x)是二次函数,最多有两个零点,
因此函数f(x)的两个零点分别位于区间(a,b),(b,c)内.
故选A.
考点:二次函数的图象和性质,函数的零点。
点评:简单题,掌握函数零点存在定理及二次函数最多有两个零点的性质是解题的关键。

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
若定义在R上的偶函数 满足
满足 且
且 时,
时,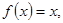 则方程
则方程 的零点个数是( )
的零点个数是( )
| A.2个 | B.3个 | C.4个 | D.多于4个 |
函数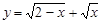 的定义域为( )
的定义域为( )
A.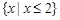 | B.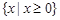 | C. | D.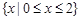 |
已知 ,符号
,符号 表示不超过
表示不超过 的最大整数,若函数
的最大整数,若函数 有且仅有3个零点,则
有且仅有3个零点,则 的取值范围是( )
的取值范围是( )
A. |
B.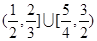 |
C. |
D. |
函数 是奇函数,图象上有一点为
是奇函数,图象上有一点为 ,则图象必过点( )
,则图象必过点( )
A. | B. | C. | D. |
已知函数 是定义在区间
是定义在区间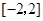 上的偶函数,当
上的偶函数,当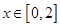 时,
时, 是减函数,如果不等式
是减函数,如果不等式 成立,求实数
成立,求实数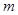 的取值范围.( )
的取值范围.( )
A.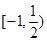 | B.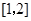 | C. | D.(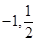 ) ) |
 是定义在R上的周期为3的周期函数,如图表示该函数在区间
是定义在R上的周期为3的周期函数,如图表示该函数在区间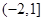 上的图像,则
上的图像,则 +
+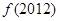 =( )
=( )
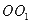 底面半径为1,高为
底面半径为1,高为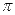 ,
,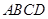 是圆柱的一个轴截面.动点
是圆柱的一个轴截面.动点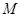 从点
从点 出发沿着圆柱的侧面到达点
出发沿着圆柱的侧面到达点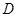 其距离最短时在侧面留下的曲线
其距离最短时在侧面留下的曲线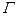 如图所示.现将轴截面
如图所示.现将轴截面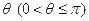 后,边
后,边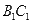 与曲线
与曲线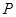 ,设
,设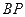 的长度为
的长度为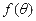 ,则
,则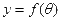 的图象大致为( )
的图象大致为( )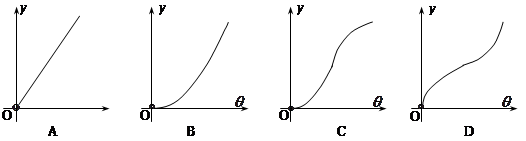
 满足
满足 ,那么函数
,那么函数 的图象大致为( )
的图象大致为( )