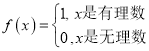题目内容
【题目】若无穷数列![]() 满足
满足![]() 对所有正整数
对所有正整数![]() 成立,则称
成立,则称![]() 为“
为“![]() 数列”,现已知数列
数列”,现已知数列![]() 是“
是“![]() 数列”.
数列”.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() 对所有
对所有![]() 成立,且存在
成立,且存在![]() 使得
使得![]() ,求
,求![]() 的所有可能值,并求出相应的
的所有可能值,并求出相应的![]() 的通项公式;
的通项公式;
(3)数列![]() 满足
满足![]() ,证明:
,证明:![]() 是等比数列当且仅当
是等比数列当且仅当![]() 是等差数列。
是等差数列。
【答案】(1)![]() 或
或![]()
(2)![]() ,
,![]()
(3)证明见解析
【解析】
(1)根据已知条件列方程求解即可;
(2)先由已知猜想![]() ,再结合与正整数有关的命题的证明,通常考虑用数学归纳法即可得证;
,再结合与正整数有关的命题的证明,通常考虑用数学归纳法即可得证;
(3)按数列![]() 是否为等差数列分类证明,可以用反证法来证明结论.
是否为等差数列分类证明,可以用反证法来证明结论.
解:(1)由已知可得:![]() ,
,
又![]() ,即
,即![]() ,
,
解得![]() 或
或![]() ;
;
(2)当![]() 时,
时,![]() ,又
,又![]() ,
,
则![]() ,则
,则![]() 与已知矛盾,
与已知矛盾,
即![]() ,
,
当![]() ,可得
,可得![]() ,
,![]() ,
,
猜想:![]() ,
,
证明:①当![]() 时,
时,![]() 成立,
成立,
② 假设当![]() ,
,![]() 时,结论成立,即
时,结论成立,即![]() ,
,
![]() ,
,
那么当![]() 时,
时,![]() ,依然成立,
,依然成立,
综上可得:![]() ;
;
(3)假设![]() 是等差数列,令
是等差数列,令![]() ,则
,则![]()
![]() ,
,
即![]()
![]()
![]()
![]() ,可得
,可得![]() ,
,
则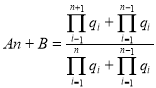 ,化简整理得:
,化简整理得:![]() 成立,
成立,
因为![]() 且
且![]() ,则
,则![]() ,则
,则![]() ,则
,则![]() 为非零的常数列的等差数列,从而得证,
为非零的常数列的等差数列,从而得证,
若![]() 不是等差数列,则
不是等差数列,则![]() ,(含变量
,(含变量![]() 的式子,非常数),
的式子,非常数),
则![]()
![]()
![]() ,根据累加法可得
,根据累加法可得![]() 常数,
常数,
故![]() 不可能是等比数列,
不可能是等比数列,
故![]() 是等比数列当且仅当
是等比数列当且仅当![]() 是等差数列.
是等差数列.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目