题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,右焦点为
,右焦点为![]() ,左顶点为A,右顶点B在直线
,左顶点为A,右顶点B在直线![]() 上.
上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设点P是椭圆C上异于A,B的点,直线![]() 交直线
交直线![]() 于点
于点![]() ,当点
,当点![]() 运动时,判断以
运动时,判断以![]() 为直径的圆与直线PF的位置关系,并加以证明.
为直径的圆与直线PF的位置关系,并加以证明.
【答案】(Ⅰ)![]() ;(Ⅱ)以BD为直径的圆与直线PF相切.
;(Ⅱ)以BD为直径的圆与直线PF相切.
【解析】
(Ⅰ)根据条件解得a,b值,(Ⅱ)设点P(x0,y0),解得D点坐标,即得以BD为直径的圆圆心坐标以及半径,再根据直线PF方程,利用圆心到直线PF距离与半径大小关系作判断.
(Ⅰ)依题可知B(a,0),a=2,因为![]() ,所以c=1,
,所以c=1,![]()
故椭圆C的方程为![]() .
.
(Ⅱ)以BD为直径的圆与直线PF相切.
证明如下:设点P(x0,y0),则![]()
①当x0=1时,点P的坐标为(1,±![]() ),直线PF的方程为x=1,
),直线PF的方程为x=1,
D的坐标为(2,±2).
此时以BD为直径的圆![]() 与直线PF相切.
与直线PF相切.
②当![]() ≠1时直线AP的方程为
≠1时直线AP的方程为![]() ,
,
点D的坐标为![]() ,BD中点E的坐标为
,BD中点E的坐标为![]() ,故
,故![]()
直线PF的斜率为![]() ,
,
故直线PF的方程为![]() ,即
,即![]() ,
,
所以点E到直线PF的距离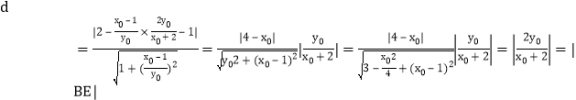 ,故以BD为直径的圆与直线PF相切.
,故以BD为直径的圆与直线PF相切.
综上得,当点P运动时,以BD为直径的圆与直线PF相切.

练习册系列答案
相关题目