题目内容
【题目】《最强大脑》是大型科学竞技类真人秀节目,是专注传播脑科学知识和脑力竞技的节目.某机构为了了解大学生喜欢《最强大脑》是否与性别有关,对某校的100名大学生进行了问卷调查,得到如下列联表:
喜欢《最强大脑》 | 不喜欢《最强大脑》 | 合计 | |
男生 | 15 | ||
女生 | 15 | ||
合计 |
已知在这100人中随机抽取1人抽到不喜欢《最强大脑》的大学生的概率为0.4
(I)请将上述列联表补充完整;判断是否有99.9%的把握认为喜欢《最强大脑》与性别有关,并说明理由;
(II)已知在被调查的大学生中有5名是大一学生,其中3名喜欢《最强大脑》,现从这5名大一学生中随机抽取2人,抽到喜欢《最强大脑》的人数为X,求X的分布列及数学期望.
参考公式: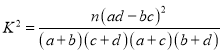 ,
,![]()
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .
.
【答案】(Ⅰ)有99.9%的把握认为喜欢《最强大脑》与性别有关;(II)见解析
【解析】
(Ⅰ)根据已知条件计算出2×2 列联表中各个数据,求出K2,可得答案;
(II)X的可能取值为0,1,2,分别求出相应的概率,由此能求出X的分布列和EX.
(Ⅰ)满足题意的2×2 列联表如下表所示:
喜欢《最强大脑》 | 不喜欢《最强大脑》 | 合计 | |
男生 | 45 | 15 | 60 |
女生 | 15 | 25 | 40 |
合计 | 60 | 40 | 100 |
由列联表中的数据,得到![]()
因此,有99.9%的把握认为喜欢《最强大脑》与性别有关.
(II)X的可能取值为0,1,2,
P(X=0)![]() ,
,
P(X=1)=![]() ,
,
P(X=2)=![]() ,
,
∴X的分布列为:
X | 0 | 1 | 2 |
P |
|
|
|
EX=![]() .
.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案【题目】某工厂因排污比较严重,决定着手整治,一个月时污染度为![]() ,整治后前四个月的污染度如下表:
,整治后前四个月的污染度如下表:
月数 |
|
|
|
| … |
污染度 |
|
|
|
| … |
污染度为![]() 后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:
后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:![]() ,
,![]() ,
,![]() ,其中
,其中![]() 表示月数,
表示月数,![]() 、
、![]() 、
、![]() 分别表示污染度.
分别表示污染度.
(1)问选用哪个函数模拟比较合理,并说明理由;
(2)若以比较合理的模拟函数预测,整治后有多少个月的污染度不超过![]() .
.