Question

【题目】已知椭圆C：1（a＞b＞0），椭圆C上的点到焦点距离的最大值为9，最小值为1．

（1）求椭圆C的标准方程；

（2）求椭圆C上的点到直线l：4x﹣5y+40＝0的最小距离？

Answer 1

【答案】（1）．（2）．

【解析】

(1)根据题意列出方程组,求出,,,从而求出椭圆的标准方程.

(2)由题可知直线与椭圆不相交,将直线平移,可知其与椭圆相切时,切点到直线的距离最小或最大,据此可设直线平行于直线,将之与椭圆方程联立,进而得解.

(1)因为椭圆C上的点到焦点距离的最大值为9,最小值为1,

所以a+c=9,a﹣c=1,

∴a=5,c=4,

∴b2=a2﹣c2=9,

∴椭圆的标准方程为:;

(2)由直线l的方程与椭圆的方程可以知道,直线l与椭圆不相交,

设直线m平行于直线l,则直线m的方程可以写成4x﹣5y+k=0,

联立,整理得25x2+8kx+k2﹣225=0,

令△=0,得64k2﹣4×25(k2﹣225)=0

解得k1=25或k2=﹣25,

∴当k1=25时,直线m与椭圆交点到直线l的距离最近,

此时直线m的方程为4x﹣5y+25=0,

直线m与直线l间的距离d,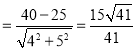

所以,椭圆C上的点到直线l:4x﹣5y+40=0的最小距离是.