题目内容
已知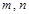 为两条不同直线,
为两条不同直线,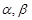 为两个不同平面,给出下列命题: ( )
为两个不同平面,给出下列命题: ( )
①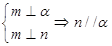 ②
②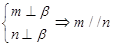
③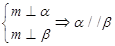 ④
④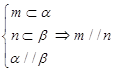
其中的正确命题序号
| A.③④ | B.②③ |
| C.①② | D.①②③④ |
B
解析试题分析:①不正确,因为还有可能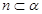 ; ②③均正确,线面垂直的性质定理;④不正确,因为两直线还有可能异面。
; ②③均正确,线面垂直的性质定理;④不正确,因为两直线还有可能异面。
考点:1线线位置关系、线面位置关系;2线线垂直、线面垂直;3线线平行、线面平行。

练习册系列答案
相关题目
已知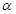 、
、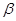 是不重合的平面,
是不重合的平面, 、
、 、
、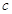 是不重合的直线,给出下列命题:
是不重合的直线,给出下列命题:
①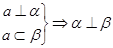 ;②
;②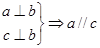 ;③
;③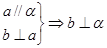 .
.
其中正确命题的个数是( )
| A.3 | B.2 | C.1 | D.0 |
正方体ABCD-A1B1C1D1中,若E是线段A1C1上一动点,那么直线CE恒垂直于
| A.AC | B.BD | C.A1D | D.A1D1 |
如图,在三棱锥 中,
中, 在
在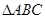 内,
内,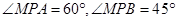 ,则
,则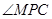 的度数为( )
的度数为( )
A. | B. | C.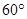 | D. |
工人师傅想对如右图的直角铁皮,用一条直线m 将其分成面积相等的两部分.下面是甲、乙、丙、丁四位同学给出的做法,其中做法正确的学生数是( )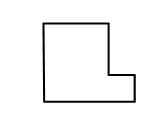
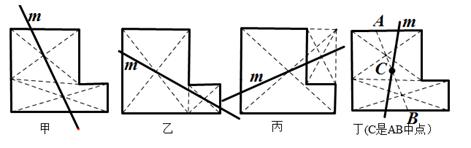
| A.4个 | B.3个 | C.2个 | D.1个 |
已知α,β,γ是三个不同的平面,命题“α∥β,且α⊥γ⇒β⊥γ”是真命题,如果把α,β,γ中的任意两个换成直线,另一个保持不变,在所得的所有新命题中,真命题有( )
| A.0个 | B.1个 | C.2个 | D.3个 |
设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是 ( ).
| A.若α⊥β,m?α,n?β,则m⊥n |
| B.若α∥β,m?α,n?β,,则m∥n |
| C.若m⊥n,m?α,n?β,则α⊥β |
| D.若m⊥α,m∥n,n∥β,则α⊥β |
如图所示,在四边形A-BCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成三棱锥ABCD,则在三棱锥ABCD中,下列命题正确的是( ).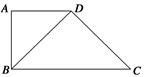
| A.平面ABD⊥平面ABC |
| B.平面ADC⊥平面BDC |
| C.平面ABC⊥平面BDC |
| D.平面ADC⊥平面ABC |
已知直线l⊥平面α,直线m?平面β,给出下列命题:
①α∥β⇒l⊥m;②α⊥β⇒l∥m;③l∥m⇒α⊥β;④l⊥m⇒α∥β,其中正确的命题是( ).
| A.①②③ | B.②③④ | C.②④ | D.①③ |