题目内容
已知圆C在x轴上的截距为-1和3,在y轴上的一个截距为1。
(1)求圆C的方程;
(2)若过点M(2, -1)的直线l被圆C截得的弦AB的长为4,求直线l的倾斜角。
-1)的直线l被圆C截得的弦AB的长为4,求直线l的倾斜角。
(1)求圆C的方程;
(2)若过点M(2,
 -1)的直线l被圆C截得的弦AB的长为4,求直线l的倾斜角。
-1)的直线l被圆C截得的弦AB的长为4,求直线l的倾斜角。解:(1)圆C在x轴上的截距为-1和3,在y轴上的一个截距为1,
∴圆C过点A(-1,0)、B(3,0),C(0,1),
∴圆心在线段AB的中垂线x=1上,且在AC的中垂线y=-x上,
∴圆心为(1,-1),
∴圆C的半径r=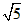 ,
,
从而,圆C的方程为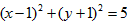 ;
;
(2)设直线l的斜率为k,则直线l的方程为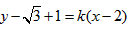 ,
,
∵弦AB的长为4,圆C的半径r=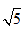 ,
,
∴圆心(1,-1)到直线l的距离为1,
∴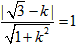 ,解得
,解得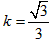 ,
,
另外,当直线的斜率k不存在时,直线x=2也满足条件,
所以直线的倾斜角为30°或90°。
∴圆C过点A(-1,0)、B(3,0),C(0,1),
∴圆心在线段AB的中垂线x=1上,且在AC的中垂线y=-x上,
∴圆心为(1,-1),
∴圆C的半径r=
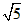 ,
, 从而,圆C的方程为
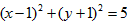 ;
;(2)设直线l的斜率为k,则直线l的方程为
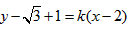 ,
,∵弦AB的长为4,圆C的半径r=
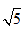 ,
,∴圆心(1,-1)到直线l的距离为1,
∴
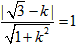 ,解得
,解得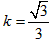 ,
,另外,当直线的斜率k不存在时,直线x=2也满足条件,
所以直线的倾斜角为30°或90°。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目