题目内容
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.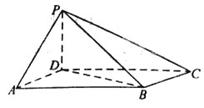
(Ⅰ) 证明:PA⊥BD;
(Ⅱ) 若PD=AD,求二面角A-PB-C的余弦值。
(Ⅰ)由余弦定理得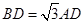 ,证得BD2+AD2= AB2,故BD
,证得BD2+AD2= AB2,故BD AD;可得 BD
AD;可得 BD  PD
PD
所以BD  平面PAD. 故 PA
平面PAD. 故 PA BD
BD
(Ⅱ)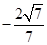
解析试题分析:(Ⅰ)因为 , 由余弦定理得
, 由余弦定理得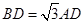
从而BD2+AD2= AB2,故BD AD;又PD
AD;又PD  底面ABCD,可得BD
底面ABCD,可得BD  PD
PD
所以BD  平面PAD. 故 PA
平面PAD. 故 PA BD
BD
(Ⅱ)如图,以D为坐标原点,AD的长为单位长,射线DA为 轴的正半轴建立空间直角坐标系D-
轴的正半轴建立空间直角坐标系D-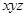 ,则
,则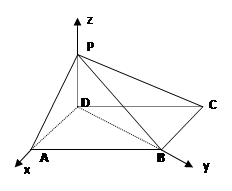
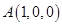 ,
,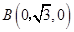 ,
,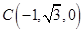 ,
,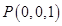 。
。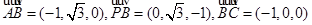
设平面PAB的法向量为n=(x,y,z),则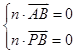 ,
,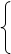 即
即 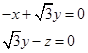
因此可取n=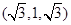
设平面PBC的法向量为m,则 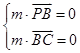
可取m=(0,-1,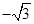 )
) 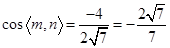
故二面角A-PB-C的余弦值为 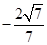
考点:本题主要考查立体几何中的垂直关系、角的计算。
点评:典型题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤,利用空间向量,省去繁琐的证明,也是解决立体几何问题的一个基本思路。注意运用转化与化归思想,将空间问题转化成平面问题。

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 中,
中,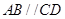 ,
,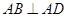 ,
,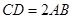 ,平面
,平面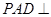 底面
底面 ,
,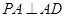 .
.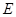 和
和 分别是
分别是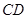 和
和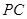 的中点,求证:
的中点,求证:
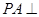 底面
底面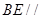 平面
平面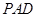 ;
;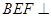 平面
平面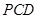 .
.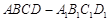 中,
中,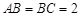 ,过
,过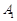 、
、 、
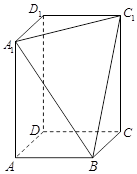
、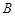 三点的平面截去长方体的一个角后,得到如图所示的几何体
三点的平面截去长方体的一个角后,得到如图所示的几何体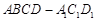 ,且这个几何体的体积为
,且这个几何体的体积为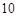 .
.
 的长;
的长;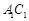 的中点为
的中点为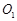 ,求异面直线
,求异面直线 与
与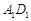 所成角的大小(结果用反三角函数值表示).
所成角的大小(结果用反三角函数值表示). 中
中 ,
, 面
面 ,
, ,
, 面
面 .
.
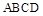 与
与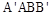 都是边长为
都是边长为 的正方形,点E是
的正方形,点E是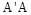 的中点,
的中点,
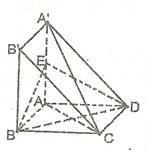
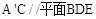 ;
;  ;
;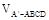 与
与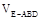 的比值。
的比值。 中,平面
中,平面 平面
平面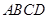 ,
, ,
, ,
, ,
, 是
是 中点,
中点, 是
是 中点.
中点. 
 平面
平面 ;
; 的体积.
的体积. 中,M、N分别是BC、AC1中点,AA1=2,AB=
中,M、N分别是BC、AC1中点,AA1=2,AB=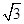 ,AC=AM=1.
,AC=AM=1.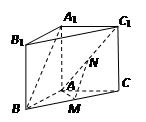
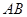 是半圆
是半圆 的直径,
的直径,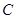 是半圆
是半圆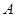 、
、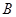 外的一个动点,
外的一个动点, 垂直于半圆
垂直于半圆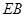 ,
,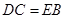 ,
,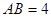 ,
, .
.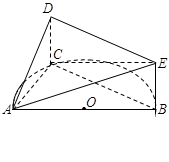
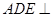 平面
平面 ;
;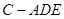 体积最大时,求二面角
体积最大时,求二面角 的余弦值.
的余弦值.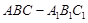 中,
中,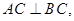
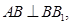
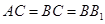 ,
,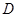 为
为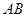 的中点,且
的中点,且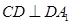 .
.
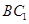 ∥平面
∥平面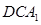 ;
;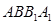 所成角的大小.
所成角的大小.