题目内容
设f(x)=2x3+ax2+bx+1的导数为f′(x),若函数y=f′(x)的图象关于直线x=-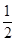 对称,且f′(1)=0.
对称,且f′(1)=0.
(1)求实数a,b的值;
(2)讨论函数f(x)的单调性,并求出单调区间 。
【答案】
(1)a=3、 b=—12;(2) 单调等增区间为(-∞,-2)和(1,+∞),单调递减区间为(-2,1)。
【解析】
试题分析:(1) 因为f′(x)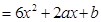 的图象关于直线x=-
的图象关于直线x=-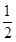 对称,所以
对称,所以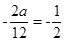 ,所以a=3;又f′(1)=0,所以b=—12。
,所以a=3;又f′(1)=0,所以b=—12。
(2)由(1)知,知f(x)=2x3+3x2-12x+1,所以f′(x)=6x2+6x-12=6(x-1)(x+2),
令f′(x)=0,得x=1或x=-2,
当x∈(-∞,-2)时,f′(x)>0,f(x)在(-∞,-2)上是增函数;
当x∈(-2,1)时,f′(x)<0,f(x)在(-2,1)上是减函数;
当x∈(1,+∞)时,f′(x)>0,f(x)在(1,+∞)上是增函数。
所以f(x)的单调等增区间为(-∞,-2)和(1,+∞),单调递减区间为(-2,1)。
考点:本题考查利用导数研究函数的单调性;二次函数的性质。
点评:当f(x)不含参数时,可通过解不等式f′(x)>0(或f′(x)<0)直接得到单调递增(或单调递减)区间。但要注意函数的定义域。

练习册系列答案
相关题目