题目内容
16.(1)对一切实数x不等式(m+1)x2-2(m+1)x-m≤0恒成立,求m的取值范围;(2)对一切实数x不等式(m+1)x2-2(m+1)x-m<0恒成立,求m的取值范围;
(3)对一切实数x不等式(m+1)x2-2(m+1)x-m≥0恒成立,求m的取值范围;
(4)求函数y=(m+1)x2-2(m+1)x-m≥0的最值?(其中m为常数)
分析 (1)根据题意,对字母系数m进行讨论,求出对应m的取值范围;
(2)根据题意,对字母系数m进行讨论,求出对应m的取值范围;
(3)根据题意,讨论m的取值,列出对应的不等式,求出m的取值范围;
(4)讨论m+1>0?=0?还是<0?,求出对应函数y的最值.
解答 解:(1)当m+1=0时,m=-1,不等式化为1≤0,显然不成立;
当m+1≠0,即m≠-1时,应满足$\left\{\begin{array}{l}{m+1<0}\\{△≤0}\end{array}\right.$,
即$\left\{\begin{array}{l}{m<-1}\\{{4(m+1)}^{2}-4(m+1)•(-m)≤0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m<-1}\\{-1≤m≤-\frac{1}{2}}\end{array}\right.$,
此不等式组无解,
∴m的取值范围是∅;
(2)当m+1=0时,m=-1,不等式化为1<0,显然不成立;
当m+1≠0,即m≠-1时,应满足$\left\{\begin{array}{l}{m+1<0}\\{△<0}\end{array}\right.$,
即$\left\{\begin{array}{l}{m<0}\\{{4(m+1)}^{2}-4(m+1)•(-m)<0}\end{array}\right.$;
解得$\left\{\begin{array}{l}{m<-1}\\{-1<m<-\frac{1}{2}}\end{array}\right.$,
此不等式组无解,
∴m的取值范围是∅;
(3)当m+1=0,即m=-1时,不等式化为1≥0,恒成立;
当m+1≠0,即m≠-1时,应满足$\left\{\begin{array}{l}{m+1>0}\\{△≤0}\end{array}\right.$,
即$\left\{\begin{array}{l}{m>-1}\\{{4(m+1)}^{2}-4(m+1)•(-m)≤0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m>-1}\\{-1≤m≤-\frac{1}{2}}\end{array}\right.$,
即-1<m≤$\frac{1}{2}$;
综上,m的取值范围是{m|-1≤m≤-$\frac{1}{2}$};
(4)当m+1=0时,m=-1,函数应为y=1,最大、最小值都是1;
当m+1≠0,即m≠-1时,若m+1>0,即m>-1时,
函数y=(m+1)x2-2(m+1)x-m有最小值,
为$\frac{4(m+1)•(-m)-{4(m+1)}^{2}}{4(m+1)}$=-2m-1;
若m+1<0,即m<-1时,
函数y=(m+1)x2-2(m+1)x-m有最大值,
为$\frac{4(m+1)•(-m)-{4(m+1)}^{2}}{4(m+1)}$=-2m-1.
点评 本题考查了不等式恒成立问题,也考查了求二次函数的最值问题以及分类讨论的应用问题,是综合性题目.

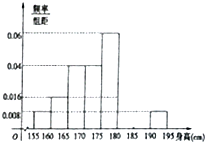 从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195].如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人,则第七组的频率为( )
从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195].如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人,则第七组的频率为( )| A. | 0.08 | B. | 0.016 | C. | 0.06 | D. | 0.012 |
| A. | -$\frac{9}{2}$ | B. | $\frac{9}{2}$ | C. | -2 | D. | 2 |