题目内容
已知空间四边形OABC,其对角线OB、AC,M、N分别是边OA、CB的中点,点G在线段MN上,且使MG=2GN,用向量
,
,
表示向量
是( )
| OA |
| OB |
| OC |
表示向量
| OG |
A.
| B.
| ||||||||||||||||||||||||||||
C.
| D.
|
∵
=
+
=
+
=
+
(
+
+
)
=
+
+
(
-
)
=
+
+
∴
=
+
+
故选C.
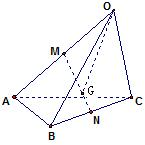
| OG |
| OM |
| MG |
| OM |
| 2 |
| 3 |
| MN |
=
| OM |
| 2 |
| 3 |
| MO |
| OC |
| CN |
=
| 1 |
| 3 |
| OM |
| 2 |
| 3 |
| OC |
| 1 |
| 3 |
| OB |
| OC |
=
| 1 |
| 6 |
| OA |
| 1 |
| 3 |
| OB |
| 1 |
| 3 |
| OC |
∴
| OG |
| 1 |
| 6 |
| OA |
| 1 |
| 3 |
| OB |
| 1 |
| 3 |
| OC |
故选C.


练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 、
、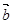 共线,则向量
共线,则向量 两两共面,则向量
两两共面,则向量 ,总存在实数
,总存在实数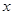 、
、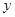 、
、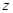 ,使得
,使得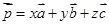 ;
;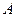 、
、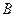 、
、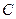 为
为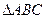 的三内角,且其对边分别为a、b、c,若
的三内角,且其对边分别为a、b、c,若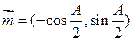 ,
,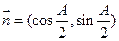 ,且
,且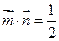 .
.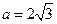 ,三角形面积
,三角形面积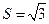 ,求
,求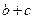 的值.
的值.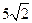 ,则︱b︱=
,则︱b︱=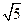
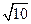
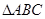 中,
中,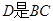 边的中点,过点
边的中点,过点 的直线分别交直线
的直线分别交直线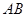 、
、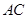 于点
于点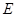 、
、 ,若
,若 ,
,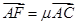 ,其中
,其中 ,则
,则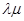 的最小值是( )
的最小值是( )
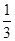

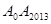 外一点,若
外一点,若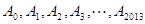 中任意相邻两点的距离相等,
中任意相邻两点的距离相等,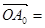 a,
a,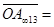 b用a,b表示
b用a,b表示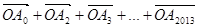 其结果为( )
其结果为( )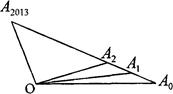
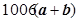


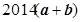
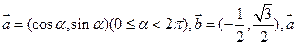 与
与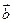 不共线,
不共线,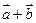 与
与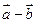 垂直
垂直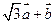 与
与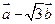 的模相等,求角
的模相等,求角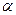 .
.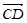 =
= ,则λ=( ).
,则λ=( ).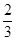 B.
B.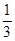 C.-
C.-