题目内容
 t∈R,且t∈(0,10),由t确定两个任意点P(t,t),Q(10-t,0).
t∈R,且t∈(0,10),由t确定两个任意点P(t,t),Q(10-t,0).(1)直线PQ是否能通过下面的点M(6,1),点N(4,5);
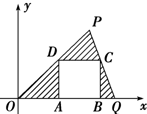
(2)在△OPQ内作内接正方形ABCD,顶点A、B在边OQ上,顶点C在边PQ上,顶点D在边OP上.
①求证:顶点C一定在直线y=
 x上.
x上.②求下图中阴影部分面积的最大值,并求这时顶点A、B、C、D的坐标.
【答案】分析:对于(1)可先求直线PQ的方程再把点M,点N的坐标代入检验即可得到结论.
对于(2)的①找出点C的坐标看是否适合直线y= x.对于(2)的②阴影部分的面积即为三角形的面积减去正方形的面积,作差求最值即可.
x.对于(2)的②阴影部分的面积即为三角形的面积减去正方形的面积,作差求最值即可.
解答:解:(1)令过P、Q方程
tx-2(t-5)y+t2-10t=0,
假设M过PQ,
则t2-6t+10=0,△=36-40<0,无实根,故M不过直线PQ.
若假设N过直线PQ,
同理得:t2-16t+50=0,t1=8- ,t2=8+
,t2=8+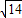 (舍去)
(舍去)
∵t∈(0,10),当t=8-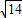 时,直线PQ过点N(4,5)
时,直线PQ过点N(4,5)
(2)由已知条件可设A(a,0),B(2a,0),C(2a,a),D(a,a).
①点C(2a,a),即 ,
,
消去a得y= x,
x,
故顶点C在直线y= x上.
x上.
②令阴影面积为S,则s= |10-t|-|t|-a2
|10-t|-|t|-a2
∵t>0,10-t>0,S= (-t2+10t)-a2
(-t2+10t)-a2
∵点C(2a,a)在直线PQ上,
∴2at-2(t-5)a=-t2+10t
∴a= (10t-t2),
(10t-t2),
S= ×10a-a2=-
×10a-a2=- +
+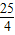
∴当a= 时,Smax=
时,Smax=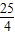 ,
,
此时顶点A、B、C、D的坐标为A( ,0)
,0)
,B(5,0),C(5, ),D(
),D( ,
, )
)
点评:转化思想是我们高中常考的一种解题思想,常用于正面不好求,但转化后好求的题中.
对于(2)的①找出点C的坐标看是否适合直线y=
 x.对于(2)的②阴影部分的面积即为三角形的面积减去正方形的面积,作差求最值即可.
x.对于(2)的②阴影部分的面积即为三角形的面积减去正方形的面积,作差求最值即可.解答:解:(1)令过P、Q方程

tx-2(t-5)y+t2-10t=0,
假设M过PQ,
则t2-6t+10=0,△=36-40<0,无实根,故M不过直线PQ.
若假设N过直线PQ,
同理得:t2-16t+50=0,t1=8-
 ,t2=8+
,t2=8+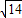 (舍去)
(舍去)∵t∈(0,10),当t=8-
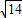 时,直线PQ过点N(4,5)
时,直线PQ过点N(4,5)(2)由已知条件可设A(a,0),B(2a,0),C(2a,a),D(a,a).
①点C(2a,a),即
 ,
,消去a得y=
 x,
x,故顶点C在直线y=
 x上.
x上.②令阴影面积为S,则s=
 |10-t|-|t|-a2
|10-t|-|t|-a2∵t>0,10-t>0,S=
 (-t2+10t)-a2
(-t2+10t)-a2∵点C(2a,a)在直线PQ上,
∴2at-2(t-5)a=-t2+10t
∴a=
 (10t-t2),
(10t-t2),S=
 ×10a-a2=-
×10a-a2=- +
+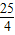
∴当a=
 时,Smax=
时,Smax=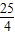 ,
,此时顶点A、B、C、D的坐标为A(
 ,0)
,0),B(5,0),C(5,
 ),D(
),D( ,
, )
)点评:转化思想是我们高中常考的一种解题思想,常用于正面不好求,但转化后好求的题中.

练习册系列答案
相关题目
 t∈R,且t∈(0,10),由t确定两个任意点P(t,t),Q(10-t,0).
t∈R,且t∈(0,10),由t确定两个任意点P(t,t),Q(10-t,0). 如图O是△ABC内的一点,
如图O是△ABC内的一点, t∈R,且t∈(0,10),由t确定两个任意点P(t,t),Q(10-t,0).
t∈R,且t∈(0,10),由t确定两个任意点P(t,t),Q(10-t,0). x上.
x上. t∈R,且t∈(0,10),由t确定两个任意点P(t,t),Q(10-t,0).
t∈R,且t∈(0,10),由t确定两个任意点P(t,t),Q(10-t,0). x上.
x上.