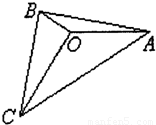
题目内容
 如图O是△ABC内的一点,
如图O是△ABC内的一点,| OA |
| OB |
| OC |
| O |
(1)若O是△ABC的重心,求k,t的值;
(2)若|
| OA| |
| OC |
| OA |
| OB |
求△BOC与△BAC的面积之比.
分析:(1)根据O是△ABC的重心,易延长AO到E,使OE=AO,交BC于D,易得
+
+
=
,进而根据平面向量的基本定理,得到k,t的值;
(2)由已知分别求出∠BOC和|
,代入到三角形面积公式,求出△BOC与△BAC的面积,可得答案.
| OA |
| OB |
| OC |
| 0 |
(2)由已知分别求出∠BOC和|
| OB| |
解答: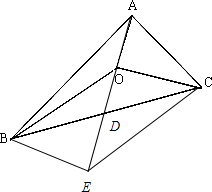 解:若O是△ABC的重心,则延长AO到E,使OE=AO,交BC于D
解:若O是△ABC的重心,则延长AO到E,使OE=AO,交BC于D
则D为BC的中点
则
=
+
=-
.
∴
+
+
=
即k=1,t=1
(2)∵|
=2,|
|=1,∠AOB=120°,∠AOC=90°,
∴∠BOC=150°,
又∵
•
=-1,即|
•|
|cos120°=-|
=-1
∴|
=1
∴S△BOC=
|
•|
|sin150°=
S△BAC=S△BOC+S△AOC+S△AOB=
+
|
•|
|sin90°+
|
•|
|sin120°=
故△BOC与△BAC的面积之比为1:5+2
 解:若O是△ABC的重心,则延长AO到E,使OE=AO,交BC于D
解:若O是△ABC的重心,则延长AO到E,使OE=AO,交BC于D则D为BC的中点
则
| OE |
| OB |
| OC |
| OA |
∴
| OA |
| OB |
| OC |
| 0 |
即k=1,t=1
(2)∵|
| OA| |
| OC |
∴∠BOC=150°,
又∵
| OA |
| OB |
| OA| |
| OB |
| OB| |
∴|
| OB| |
∴S△BOC=
| 1 |
| 2 |
| OB| |
| OC |
| 1 |
| 4 |
S△BAC=S△BOC+S△AOC+S△AOB=
| 1 |
| 4 |
| 1 |
| 2 |
| OA| |
| OC |
| 1 |
| 2 |
| OA| |
| OB |
5+2
| ||
| 4 |
故△BOC与△BAC的面积之比为1:5+2
| 3 |
点评:本题考查的知识点是微量的数量积,三角形面积公式,重心的性质,利用向量法,在求夹角和求距离时,速度快,精度高,是解答几何问题常用的方法.

练习册系列答案
相关题目
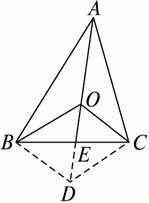
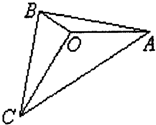 如图,O是△ABC内的一点,∠AOB=150°,∠AOC=120°,向量
如图,O是△ABC内的一点,∠AOB=150°,∠AOC=120°,向量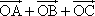 =0,求证:O是△ABC的重心.
=0,求证:O是△ABC的重心.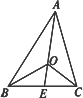
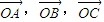 的模分别为2、1、3.
的模分别为2、1、3.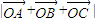 ;
;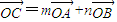 ,求实数m,n的值.
,求实数m,n的值.