题目内容
设定义域为R的函数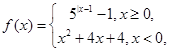 若关于x的方程
若关于x的方程 有7个不同的实数解,则m=( ).
有7个不同的实数解,则m=( ).
| A.2 | B.4或6 | C.2或6 | D.6 |
A
解析试题分析: 题中原方程
题中原方程 有7个不同的实数根,
有7个不同的实数根,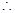 即要求对应于
即要求对应于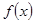 等于某个常数有3个不同实数解和4个不同的实数解,
等于某个常数有3个不同实数解和4个不同的实数解,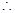 故先根据题意作出
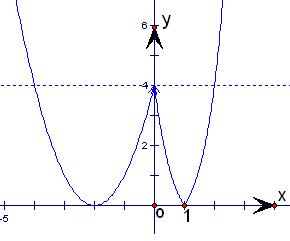
故先根据题意作出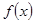 的简图:
的简图:
由图可知,只有当 时,它有三个根.
时,它有三个根.
故关于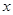 的方程
的方程 有一个实数根4.
有一个实数根4.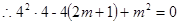 ,
,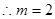 ,或
,或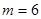 ,
,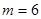 时,方程
时,方程
 或
或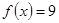 ,有5个不同的实数根,所以
,有5个不同的实数根,所以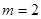 .
.
考点:函数与方程的综合运用

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
定义在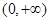 上的可导函数
上的可导函数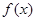 满足:
满足: 且
且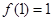 ,则不等式
,则不等式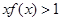 的解集为( )
的解集为( )
A.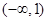 | B.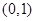 | C.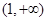 | D. |
已知 则方程
则方程 所有实根的个数是( )
所有实根的个数是( )
| A.2 | B.3 | C.4 | D.5 |
(5分)(2011•广东)函数f(x)=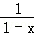 +lg(1+x)的定义域是( )
+lg(1+x)的定义域是( )
| A.(﹣∞,﹣1) | B.(1,+∞) | C.(﹣1,1)∪(1,+∞) | D.(﹣∞,+∞) |
定义在R上的偶函数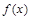 满足
满足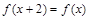 且
且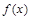 在
在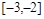 上是减函数,又
上是减函数,又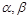 是锐角三角形的两个内角,则( )
是锐角三角形的两个内角,则( )
A.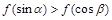 | B.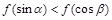 |
C.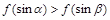 | D.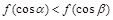 |
函数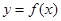 的定义域为
的定义域为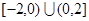 ,其图像上任一点
,其图像上任一点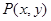 都位于椭圆
都位于椭圆 :
: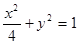 上,下列判断①函数
上,下列判断①函数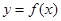 一定是偶函数;②函数
一定是偶函数;②函数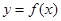 可能既不是偶函数,也不是奇函数;③函数
可能既不是偶函数,也不是奇函数;③函数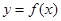 可能是奇函数;④函数
可能是奇函数;④函数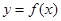 如果是偶函数,则值域是
如果是偶函数,则值域是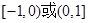 ;⑤函数
;⑤函数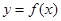 值域是
值域是 ,则一定是奇函数.其中正确的命题个数有( )个
,则一定是奇函数.其中正确的命题个数有( )个
| A.1 | B.2 | C.3 | D.4 |
已知函数f(x)=log0.5(x2-ax+3a)在[2,+∞)单调递减,则a的取值范围是( )
| A.(-∞,4] | B.[4,+∞) |
| C.[-4,4] | D.(-4,4] |
[2013·山东高考]已知函数f(x)为奇函数,且当x>0时,f(x)=x2+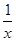 ,则f(-1)=( )
,则f(-1)=( )
| A.-2 | B.0 | C.1 | D.2 |
(2014·长沙模拟)某公司在甲、乙两地销售一种品牌车,利润(单位:万元)分别为L1=5.06x-0.15x2和L2=2x,其中x为销售量(单位:辆).若该公司在这两地共销售15辆车,则能获得的最大利润为( )
| A.45.606万元 | B.45.6万元 |
| C.45.56万元 | D.45.51万元 |