题目内容
7.求函数y=-$\frac{x}{\sqrt{{x}^{2}+2x+2}}$的值域.分析 分类得出当x=0时,y=0;当x<0时y=$\frac{1}{\sqrt{2\frac{1}{{x}^{2}}+2\frac{1}{x}}+1}$,换元得出设t=$\frac{1}{x}$,则t<0,m=2t2+2t+1,在(-∞,-$\frac{1}{2}$)上单调递减,(-$\frac{1}{2}$,0)单调递增,y=$\frac{1}{\sqrt{m}}$
当x>0时,y=-$\frac{1}{\sqrt{2\frac{1}{{x}^{2}}+2\frac{1}{x}}+1}$,设t=$\frac{1}{x}$,则t>0,m=2t2+2t+1,在(0,+∞)单调递增,m>1,y=-$\frac{1}{\sqrt{m}}$,再分别利用二次函数的单调性求解即可.
解答 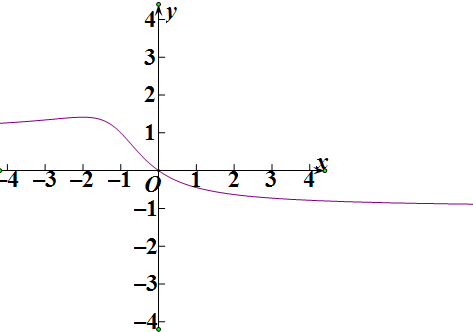 解:∵函数y=-$\frac{x}{\sqrt{{x}^{2}+2x+2}}$,的定义域为R,
解:∵函数y=-$\frac{x}{\sqrt{{x}^{2}+2x+2}}$,的定义域为R,
∴当x=0时,y=0,
当x<0时,y=$\frac{\sqrt{{x}^{2}}}{\sqrt{{x}^{2}+2x+2}}$=$\frac{1}{\sqrt{2\frac{1}{{x}^{2}}+2\frac{1}{x}}+1}$,
设t=$\frac{1}{x}$,则t<0,m=2t2+2t+1,在(-∞,-$\frac{1}{2}$)上单调递减,(-$\frac{1}{2}$,0)单调递增,
y=$\frac{1}{\sqrt{m}}$,
m≥2×$\frac{1}{4}$=$\frac{1}{2}$,
根据函数y=$\frac{1}{\sqrt{x}}$的单调性得出:0$<y≤\sqrt{2}$,
当x>0时,y=-$\frac{1}{\sqrt{2\frac{1}{{x}^{2}}+2\frac{1}{x}}+1}$,
设t=$\frac{1}{x}$,则t>0,m=2t2+2t+1,在(0,+∞)单调递增,
∴m>1,y=-$\frac{1}{\sqrt{m}}$
即得出:-1<y<0,
综上得出:函数y=-$\frac{x}{\sqrt{{x}^{2}+2x+2}}$的值域为(-1,$\sqrt{2}$]
点评 本题考查了较复杂的函数的值域的求解,分类讨论的思想,利用函数单调性求解值域,换元法思想,属于中档题.

| A. | α+β<π | B. | α+β>$\frac{3π}{2}$ | C. | α+β=$\frac{3π}{2}$ | D. | α+β<$\frac{3π}{2}$ |