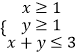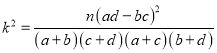题目内容
【题目】正三棱台的上、下底面的边长分别是3和6. 
(1)若侧面与底面所成的角为60°,求此三棱台的体积;
(2)若侧棱与底面所成的角为60°,求此三棱台的侧面积.
【答案】
(1)解:如图,
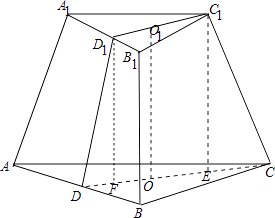
作C1D1⊥A1B1,CD⊥AB,作C1E⊥CD=E,D1F⊥CD=F,
∵上底面边长为3,∴上底面边A1B1上的高 ![]() ,
,
则 ![]() ,
,
∵下底面边长为6,∴下底面边AB上的高为CD= ![]() ,
,
则 ![]() ,
,
∴ ![]() ,
, ![]() ,
,
上底面面积为 ![]() ,下底面面积为
,下底面面积为 ![]() .
.
若正三棱台侧面与底面成60°,即∠D1DF=60°,
∴三棱台的高为 ![]() ,
,
则三棱台体积V= ![]() =
= ![]()
(2)解:若正三棱台侧棱与底面成60°,即∠C1CE=60°,
∴三棱台的高为 ![]() ,
,
则三棱台的斜高为 ![]() ,
,
∴此三棱台的侧面积为3× ![]()
【解析】由题意画出图形,由已知求出上下底面面积.(1)当侧面与底面所成的角为60°时,解三角形求出棱台的高,代入体积公式得答案;(2)当侧棱与底面所成的角为60°时,解三角形求出棱台的斜高,代入侧面积公式得答案.

 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
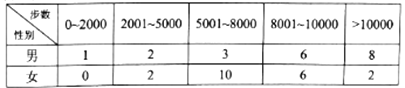
快乐暑假暑假能力自测中西书局系列答案【题目】为提高市场销售业绩,某公司设计两套产品促销方案(方案1运作费用为![]() 元/件;方案2的的运作费用为
元/件;方案2的的运作费用为![]() 元/件),并在某地区部分营销网点进行试点(每个试点网点只采用一种促销方案),运作一年后,对比该地区上一年度的销售情况,分别统计相应营销网点个数,制作相应的列联表如下表所示.
元/件),并在某地区部分营销网点进行试点(每个试点网点只采用一种促销方案),运作一年后,对比该地区上一年度的销售情况,分别统计相应营销网点个数,制作相应的列联表如下表所示.
无促销活动 | 采用促销方案1 | 采用促销方案2 | ||
本年度平均销售额不高于上一年度平均销售额 | 48 | 11 | 31 | 90 |
本年度平均销售额高于上一年度平均销售额 | 52 | 69 | 29 | 150 |
100 | 80 | 60 |
(Ⅰ)请根据列联表提供的信息,为该公司今年选择一套较为有利的促销方案(不必说明理由);
(Ⅱ)已知该公司产品的成本为10元/件(未包括促销活动运作费用),为制定本年度该地区的产品销售价格,统计上一年度的![]() 组售价
组售价![]() (单位:元/件,整数)和销量
(单位:元/件,整数)和销量![]() (单位:件)(
(单位:件)(![]() )如下表所示:
)如下表所示:
售价 |
|
|
|
|
|
|
|
|
销量 |
|
|
|
|
|
|
|
|
(ⅰ)请根据下列数据计算相应的相关指数![]() ,并根据计算结果,选择合适的回归模型进行拟合;
,并根据计算结果,选择合适的回归模型进行拟合;
(ⅱ)根据所选回归模型,分析售价![]() 定为多少时?利润
定为多少时?利润![]() 可以达到最大.
可以达到最大.
|
|
| |
|
|
|
|
|
| ||
参考公式:相关指数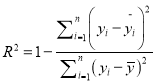 .
.