题目内容
1. 如图,已知动圆M过定点F(1,0)且与y轴相切,点F关于圆心M的对称点为F′,点F′的轨迹为H.
如图,已知动圆M过定点F(1,0)且与y轴相切,点F关于圆心M的对称点为F′,点F′的轨迹为H.(1)求曲线H的方程;
(2)一条直线AB经过点F,且交曲线H于A、B两点,点C为直线x=1上的动点.
①求证:∠ACB不可能是钝角;
②是否存在这样的点C,使得△ABC是正三角形?若存在,求点C的坐标;否则,说明理由.
分析 (1)设F′(x,y),则可得M($\frac{x+1}{2}$,$\frac{y}{2}$),圆M的直径为|FF′|=$\sqrt{(x-{1)}^{2}+{y}^{2}}$,利用动圆M与y轴相切,即可求得曲线C的方程;
(2)①设直线AB:x=my+1,A(x1,y1),B(x2,y2),C(-1,n),联立直线与抛物线方程,进而利用韦达定理结合向量的数量积运算,得到$\overrightarrow{CA}$•$\overrightarrow{CB}$≥0恒成立,可得结论;
②由①知M(2m2+1,2m),根据CM与AB垂直,斜率积为-1,可得n=2m3+4m,再由|CM|=$\frac{\sqrt{3}}{2}$|AB|,求出m值.
解答 解:(1)设F′(x,y),因为点F(1,0)在圆M上,且点F关于圆心M的对称点为F,
则M($\frac{x+1}{2}$,$\frac{y}{2}$),而|FF′|=$\sqrt{(x-{1)}^{2}+{y}^{2}}$,
则$\frac{1}{2}$$\sqrt{(x-{1)}^{2}+{y}^{2}}$=$\frac{1}{2}$|x+1|,
化简得:y2=4x,所以曲线C的方程为y2=4x…(5分)
(2)①设直线AB:x=my+1,A(x1,y1),B(x2,y2),C(-1,n)
由$\left\{\begin{array}{l}x=my+1\\{y}^{2}=4x\end{array}\right.$,得y2-4my-4=0,
则y1+y2=4m,y1•y2=-4,x1+x2=m(y1+y2)+2=4m2+2,x1•x2=m2y1•y2+m(y1+y2)+1=1…(7分)
$\overrightarrow{CA}$=(x1+1,y1-n),$\overrightarrow{CB}$=(x2+1,y2-n),
$\overrightarrow{CA}$•$\overrightarrow{CB}$=x1•x2+x1+x2+1+y1•y2-n(y1+y2)+n2=(2m-n)2≥0恒成立,
则∠ACB不可能是钝角;…(10分)
②假设存在这样的点C,由①知M(2m2+1,2m)
kCM•kAB=$\frac{2m-n}{2{m}^{2}+2}•\frac{1}{m}$=-1,则n=2m3+4m,则C(-1,2m3+4m),
则|CM|=$\sqrt{(2{m}^{2}+2)^{2}+(2{m}^{3}+2m)^{2}}$=2(m2+1)$\sqrt{{m}^{2}+1}$,
而|AB|=$\sqrt{{m}^{2}+1}$|y1-y2|=4(m2+1),由|CM|=$\frac{\sqrt{3}}{2}$|AB|得,m=$±\sqrt{2}$
所以存在点C(-1,$±8\sqrt{2}$)满足条件…(15分)
点评 本题考查轨迹方程的求解,考查直线的斜率,考查直线与抛物线的位置关系,考查学生分析解决问题的能力,属于中档题.

 天天练口算系列答案
天天练口算系列答案| A. | {x|x>1} | B. | {x|x≤-1} | C. | {x|x>1或x<-1} | D. | {x|-1≤x≤1} |
| A. | (-$\frac{π}{3}$,0) | B. | (-$\frac{π}{4}$,$\frac{π}{4}$) | C. | (0,$\frac{π}{3}$) | D. | ($\frac{π}{4}$,$\frac{π}{3}$) |
| A. | $\frac{139}{234}$ | B. | $\frac{134}{198}$ | C. | $\frac{175}{264}$ | D. | $\frac{28}{93}$ |
 已知[x]表示不大于x的最大整数,如[4.5]=4,[2]=2,执行如图程序框图,则输出的i等于( )
已知[x]表示不大于x的最大整数,如[4.5]=4,[2]=2,执行如图程序框图,则输出的i等于( ) 设函数f(x)在定义域内可导且其图象如图①所示,则导函数y=f′(x)的图象最有可能是( )
设函数f(x)在定义域内可导且其图象如图①所示,则导函数y=f′(x)的图象最有可能是( )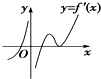



 如图所示,?ABCD的对角线AC与BD相交于点O,且AC=4,BD=2$\sqrt{3}$,AB=$\sqrt{7}$,过点D作DE⊥AB,垂足为E.请问四边形ABCD是菱形吗?请说明理由.
如图所示,?ABCD的对角线AC与BD相交于点O,且AC=4,BD=2$\sqrt{3}$,AB=$\sqrt{7}$,过点D作DE⊥AB,垂足为E.请问四边形ABCD是菱形吗?请说明理由.