题目内容
2.已知函数f(x)=sinωx-$\sqrt{3}$cosωx(ω>0)的图象与x轴的两个相邻交点的距离等于$\frac{π}{2}$,若将函数y=f(x)的图象向左平移$\frac{π}{6}$个单位得到函数y=g(x)的图象,则y=g(x)是减函数的区间为( )| A. | (-$\frac{π}{3}$,0) | B. | (-$\frac{π}{4}$,$\frac{π}{4}$) | C. | (0,$\frac{π}{3}$) | D. | ($\frac{π}{4}$,$\frac{π}{3}$) |
分析 由已知可求出函数f(x)的解析式,进而根据函数图象的平移变换法则得到函数y=g(x)的解析式,根据正弦函数的性质分析出函数的单调性后,比照四个答案即可得到结论.
解答 解:∵函数f(x)=sinωx-$\sqrt{3}$cosωx=2sin(ωx-$\frac{π}{3}$),
又∵函数f(x)=sinωx-$\sqrt{3}$cosωx(ω>0)的图象与x轴的两个相邻交点的距离等于$\frac{π}{2}$=$\frac{T}{2}$,
故函数的最小正周期T=π,
又∵ω>0,
∴ω=2,
故f(x)=2sin(2x-$\frac{π}{3}$),
将函数y=f(x)的图象向左平移$\frac{π}{6}$个单位可得y=g(x)=2sin[2(x+$\frac{π}{6}$)-$\frac{π}{3}$]=2sin2x的图象,
令$\frac{π}{2}$+2kπ≤2x≤$\frac{3π}{2}$+2kπ,即$\frac{π}{4}$+kπ≤x≤$\frac{3π}{4}$+kπ,k∈Z,
故函数y=g(x)的减区间为[$\frac{π}{4}$+kπ,$\frac{3π}{4}$+kπ],k∈Z,
当k=0时,区间[$\frac{π}{4}$,$\frac{3π}{4}$]为函数的一个单调递减区间,
又∵($\frac{π}{4}$,$\frac{π}{3}$)⊆[$\frac{π}{4}$,$\frac{3π}{4}$],
故选:D.
点评 本题考查的知识点是函数y=Asin(ωx+φ)的图象变换,两角和与差的正弦函数,正弦函数的单调性,熟练掌握正弦型函数的图象性质及变换法则是解答本题的关键,属于中档题.

练习册系列答案
相关题目
12.若关于x的不等式4ax-1<3x-4(a>0,且a≠1对于任意的x>2恒成立,则a的取值范围为( )
| A. | (0,$\frac{1}{2}$) | B. | (0,$\frac{1}{2}$] | C. | [2,+∞) | D. | (2,+∞) |
13.“x>2”是“2x>x2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
7.已知a>0,b>0,直线3x-4y=0是双曲线S:$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1的一条渐近线,双曲线S的离心率为e,则$\frac{3e+{a}^{2}}{b}$的最小值为( )
| A. | $\frac{3\sqrt{5}}{2}$ | B. | $\frac{7\sqrt{5}}{2}$ | C. | $\frac{11\sqrt{5}}{3}$ | D. | $\frac{4\sqrt{15}}{3}$ |
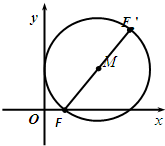 如图,已知动圆M过定点F(1,0)且与y轴相切,点F关于圆心M的对称点为F′,点F′的轨迹为H.
如图,已知动圆M过定点F(1,0)且与y轴相切,点F关于圆心M的对称点为F′,点F′的轨迹为H.