题目内容
若xi>0(i=1,2,3,…,n),观察下列不等式:(x1+x2)(
+
)≥4,(x1+x2+x3)(
+
+
)≥9,…,
请你猜测(x1+x2+…+xn)(
+
+…+
)满足的不等式,并用数学归纳法加以证明.
| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| x3 |
请你猜测(x1+x2+…+xn)(
| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| xn |
满足的不等式为(x1+x2+…+xn)(
+
+…+
)≥n2(n≥2),
证明如下:
(1)当n=2时,猜想成立;
(2)假设当n=k时,猜想成立,即(x1+x2+…+xn)(
+
+…+
)≥k2,
那么n=k+1时,(x1+x2+…+xk+1)(
+
+…+
)≥k2+2k+1=(k+1)2
则当n=k+1时猜想也成立,根据(1)(2)可得猜想对任意的n∈N,n≥2都成立.
| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| xn |
证明如下:
(1)当n=2时,猜想成立;
(2)假设当n=k时,猜想成立,即(x1+x2+…+xn)(
| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| xn |
那么n=k+1时,(x1+x2+…+xk+1)(
| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| xk |
则当n=k+1时猜想也成立,根据(1)(2)可得猜想对任意的n∈N,n≥2都成立.

练习册系列答案
相关题目
 ,数列
,数列 满足:
满足: 。
。 ;
; ;
;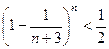 ,求证
,求证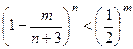 ,m=1,1,2…,n;
,m=1,1,2…,n; .
. 与Sn+1的大小,并说明理由.
与Sn+1的大小,并说明理由.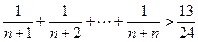 的过程中,由k推导到k+1时,不等式左边增加的式子是
的过程中,由k推导到k+1时,不等式左边增加的式子是 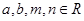 ,且
,且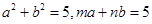 ,则
,则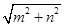 的最小值为
的最小值为 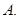
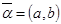 ,
,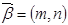 ,其中
,其中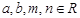 ,由不等式
,由不等式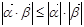 恒成立,可以证明(柯西)不等式
恒成立,可以证明(柯西)不等式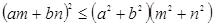 (当且仅当
(当且仅当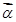 ∥
∥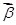 ,即
,即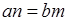 时等号成立),己知
时等号成立),己知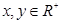 ,若
,若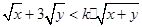 恒成立,利用可西不等式可求得实数
恒成立,利用可西不等式可求得实数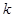 的取值范围是
的取值范围是  的最小值是 .
的最小值是 .