题目内容
(湖北理21)(本小题满分14分)
已知m,n为正整数.
(Ⅰ)用数学归纳法证明:当x>-1时,(1+x)m≥1+mx;
(Ⅱ)对于n≥6,已知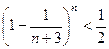 ,求证
,求证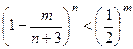 ,m=1,1,2…,n;
,m=1,1,2…,n;
(Ⅲ)求出满足等式3n+4m+…+(n+2)m=(n+3)n的所有正整数n.
已知m,n为正整数.
(Ⅰ)用数学归纳法证明:当x>-1时,(1+x)m≥1+mx;
(Ⅱ)对于n≥6,已知
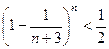 ,求证
,求证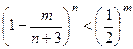 ,m=1,1,2…,n;
,m=1,1,2…,n;(Ⅲ)求出满足等式3n+4m+…+(n+2)m=(n+3)n的所有正整数n.
见解析
(Ⅲ)假设存在正整数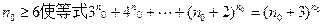 成立,
成立,
即有(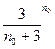 )+
)+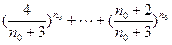 =1. ②
=1. ②
又由(Ⅱ)可得
(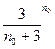 )+
)+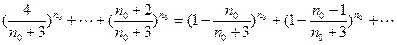
+ 与②式矛盾,
与②式矛盾,
故当n≥6时,不存在满足该等式的正整数n.
故只需要讨论n=1,2,3,4,5的情形;
当n=1时,3≠4,等式不成立;
当n=2时,32+42=52,等式成立;
当n=3时,33+43+53=63,等式成立;
当n=4时,34+44+54+64为偶数,而74为奇数,故34+44+54+64≠74,等式不成立;
当n=5时,同n=4的情形可分析出,等式不成立.
综上,所求的n只有n=2,3.
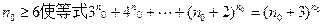 成立,
成立,即有(
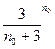 )+
)+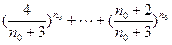 =1. ②
=1. ②又由(Ⅱ)可得
(
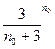 )+
)+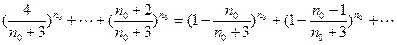
+
 与②式矛盾,
与②式矛盾,故当n≥6时,不存在满足该等式的正整数n.
故只需要讨论n=1,2,3,4,5的情形;
当n=1时,3≠4,等式不成立;
当n=2时,32+42=52,等式成立;
当n=3时,33+43+53=63,等式成立;
当n=4时,34+44+54+64为偶数,而74为奇数,故34+44+54+64≠74,等式不成立;
当n=5时,同n=4的情形可分析出,等式不成立.
综上,所求的n只有n=2,3.

练习册系列答案
相关题目
 中,
中, ,求数列
,求数列
 ,则
,则 的最小值是 .
的最小值是 .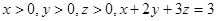 ,那么
,那么 的最小值为 ;
的最小值为 ; ”时,
”时,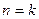 ”变到“
”变到“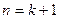 ”时,左边应增乘的因式是_________________;
”时,左边应增乘的因式是_________________;