题目内容
已知平面上的动点Q到定点F(0,1)的距离与它到定直线y=3的距离相等.(1)求动点Q的轨迹C1的方程;
(2)过点F作直线l1交C2:x2=4y于A,B两点(B在第一象限).若|BF|=2|AF|,求直线l1的方程.
(3)试问在曲线C1上是否存在一点M,过点M作曲线C1的切线l2交抛物线C2于D,E两点,使得DF⊥EF?若存在,求出点M的坐标;若不存在,请说明理由.
分析:(1)设出Q的坐标,根据条件推断出x和y的关系式,化简求得x和y的关系,即曲线的方程.
(2)设出A,B,利用抛物线的定义,表示出|AF|和|BF|,进而利用|BF|=2|AF|,求得y2和y1的关系,令直线AB的方程x=t(y-1),与抛物线方程联立消去x,表示出y1+y2和y1y2,联立求得y1和y2,代入方程②求得t,进而求得t.则直线AB的方程可得.
(3)设出M的坐标,对抛物线方程求导,进而求得切线l2的斜率,表示出l2的方程,同时利用m和n的关系式,表示出切线的方程与抛物线方程联立,设D,E的坐标,表示出x1+x2和x1x2,根据FD⊥FE,推断出x1x2+(y1-1)(y2-1)=0获得关于m的方程,求得m,进而通过m和n的关系式求得n.
(2)设出A,B,利用抛物线的定义,表示出|AF|和|BF|,进而利用|BF|=2|AF|,求得y2和y1的关系,令直线AB的方程x=t(y-1),与抛物线方程联立消去x,表示出y1+y2和y1y2,联立求得y1和y2,代入方程②求得t,进而求得t.则直线AB的方程可得.
(3)设出M的坐标,对抛物线方程求导,进而求得切线l2的斜率,表示出l2的方程,同时利用m和n的关系式,表示出切线的方程与抛物线方程联立,设D,E的坐标,表示出x1+x2和x1x2,根据FD⊥FE,推断出x1x2+(y1-1)(y2-1)=0获得关于m的方程,求得m,进而通过m和n的关系式求得n.
解答:解:(1)设Q(x,y),
由条件有
=|y-3|,
化简得曲线C1的方程为:x2=-4y+8.
(2)设A(x1,y1),B(x2,y2),则|AF|=y1+1,|BF|=y2+1,
由|BF|=2|AF|,得y2=2y1+1①
令直线AB方程为x=t(y-1)
由
?t2y2-(2t2+4)y+t2=0,
则
由①和③联立解得:y1=
,y2=2
代入②得:t2=8
依题意直线AB的斜率大于0,即t>0,
所以t=2
故直线AB的方程为x-2
y+2
=0
(3)设M(m,n),由于y′=-
,
则切线l2的斜率为k=-
,
切线l2的方程为y-n=-
(x-m),
又n=2-
,
则切线l的方程为y=-
x+
+2.
由
?x2+2mx-m2-8=0.,
设D(x1,y1),E(x2,y2),
则x1+x2=-2m
x1x2=-m2-8,
∴y1+y2=-
(x1+x2)+
+4=
+4,
y1y2=
=
.
又FD⊥FE,则x1x2+(y1-1)(y2-1)=x1x2+y1y2-(y1+y2)+1=0,
则-m2-8+
-(
+4)+1=0,
设t=m2+8,则有
-t-
(t-8)-3=0,即t2-40t+144=0,
得t=36,t=4(舍去).
所以t=m2+8=36,得m=±2
,n=-5.
故存在点M满足题意,此时点M的坐标是(±2
,-5).
由条件有
| x2+(y-1)2 |
化简得曲线C1的方程为:x2=-4y+8.
(2)设A(x1,y1),B(x2,y2),则|AF|=y1+1,|BF|=y2+1,
由|BF|=2|AF|,得y2=2y1+1①
令直线AB方程为x=t(y-1)
由
|
则
|
由①和③联立解得:y1=
| 1 |
| 2 |
代入②得:t2=8
依题意直线AB的斜率大于0,即t>0,
所以t=2
| 2 |
故直线AB的方程为x-2
| 2 |
| 2 |
(3)设M(m,n),由于y′=-
| x |
| 2 |
则切线l2的斜率为k=-
| m |
| 2 |
切线l2的方程为y-n=-
| m |
| 2 |
又n=2-
| m2 |
| 4 |
则切线l的方程为y=-
| m |
| 2 |
| m2 |
| 4 |
由
|
设D(x1,y1),E(x2,y2),
则x1+x2=-2m
x1x2=-m2-8,
∴y1+y2=-
| m |
| 2 |
| m2 |
| 2 |
| 3m2 |
| 2 |
y1y2=
| (x1x2)2 |
| 16 |
| (m2+8)2 |
| 16 |
又FD⊥FE,则x1x2+(y1-1)(y2-1)=x1x2+y1y2-(y1+y2)+1=0,
则-m2-8+
| (m2+8)2 |
| 16 |
| 3m2 |
| 2 |
设t=m2+8,则有
| t2 |
| 16 |
| 3 |
| 2 |
得t=36,t=4(舍去).
所以t=m2+8=36,得m=±2
| 7 |
故存在点M满足题意,此时点M的坐标是(±2
| 7 |
点评:本题主要考查了直线与圆锥曲线的综合问题.考查了分析推理和基本的运算能力.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
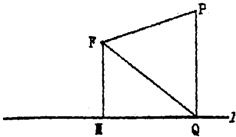 如图,平面上定点F到定直线l的距离|FM|=2,P为该平面上的动点,过P作直线l的垂线,垂足为Q,且
如图,平面上定点F到定直线l的距离|FM|=2,P为该平面上的动点,过P作直线l的垂线,垂足为Q,且