题目内容
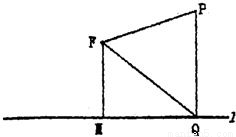
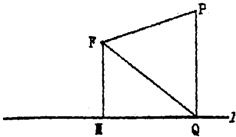如图，平面上定点F到定直线l的距离|FM|=2，P为该平面上的动点，过P作直线l的垂线，垂足为Q，且(| PF |
| PQ |
| PF |
| PQ |
（1）试建立适当的平面直角坐标系，求动点P的轨迹C的方程；
（2）过点F的直线交轨迹C于A、B两点，交直线l于点N，已知
| NA |
| AF |
| NB |
| BF |
分析：（1）方法一：先建坐标系，求出对应点的坐标直接利用向量的数量积计算即可求动点P的轨迹C的方程；
方法二：先由(
+
)•(
-
)=0得，|
|=|
|，知道动点P的轨迹是抛物线，再建坐标系求动点P的轨迹C的方程；
（2）先由已知求得λ1•λ2＜0，以及
=-
，再过A、B两点分别作准线l的垂线，利用相似比得
=
=
，二者相结合即可得λ1+λ2为定值．
方法二：先由(
| PF |
| PQ |
| PF |
| PQ |
| PQ |
| PF |
（2）先由已知求得λ1•λ2＜0，以及
|
| ||
|
|
| λ1 |
| λ2 |
|
| ||
|
|
|
| ||
|
|
|
| ||
|
|
|
| ||
|
|
解答：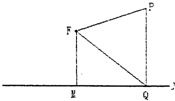
解：（1）方法一：如图，以线段FM的中点为原点O，以线段FM所在的直线为y轴建立直角坐标系xOy．则，F（0，1）．
设动点P的坐标为（x，y），则动点Q的坐标为（x，-1）
=(-x，1-y)，
=(0，-1-y)，
由(
+
)•(
-
)=0，得x2=4y．
方法二：由(
+
)•(
-
)=0得，|
|=|
|．
所以，动点P的轨迹C是抛物线，以线段FM的中点
为原点O，以线段FM所在的直线为y轴建立直角坐标系xOy，可得轨迹C的方程为：x2=4y．
（2）由已知
=λ1
，
=λ2
，得λ1•λ2＜0．
于是，
=-
，①
过A、B两点分别作准线l的垂线，垂足分别为A1、B1，
则有
=
=
，②
由①、②得λ1+λ2=0．
解：（1）方法一：如图，以线段FM的中点为原点O，以线段FM所在的直线为y轴建立直角坐标系xOy．则，F（0，1）．设动点P的坐标为（x，y），则动点Q的坐标为（x，-1）
| PF |
| PQ |
由(
| PF |
| PQ |
| PF |
| PQ |
方法二：由(
| PF |
| PQ |
| PF |
| PQ |
| PQ |
| PF |
所以，动点P的轨迹C是抛物线，以线段FM的中点
为原点O，以线段FM所在的直线为y轴建立直角坐标系xOy，可得轨迹C的方程为：x2=4y．
（2）由已知
| NA |
| AF |
| NB |
| BF |
于是，
|
| ||
|
|
| λ1 |
| λ2 |
|
| ||
|
|
过A、B两点分别作准线l的垂线，垂足分别为A1、B1，
则有
|
| ||
|
|
|
| ||
|
|
|
| ||
|
|
由①、②得λ1+λ2=0．
点评：本题考查轨迹方程的求法以及直线与抛物线的综合问题和向量的数量积．直线与圆锥曲线的位置关系，由于集中交汇了直线，圆锥曲线两章的知识内容，综合性强，能力要求高，还涉及到函数，方程，不等式，平面几何等许多知识，可以有效的考查函数与方程的思想，数形结合的思想，分类讨论的思想和转化化归的思想，因此，这一部分内容也成了高考的热点和重点．
练习册系列答案
相关题目
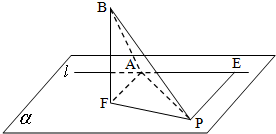如图，平面α上定点F到定直线l的距离FA=2，曲线C是平面α上到定点F和到定直线l的距离相等的动点P的轨迹． 设FB⊥α，且FB=2．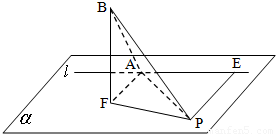
．
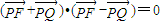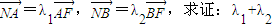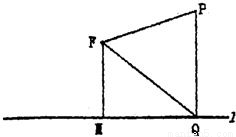
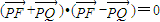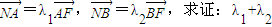为定值．
．
为定值．