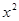题目内容
若规定 ,不等式
,不等式 对一切x∈(0,1]恒成立,则实数m的最大值为( )
对一切x∈(0,1]恒成立,则实数m的最大值为( )
 ,不等式
,不等式 对一切x∈(0,1]恒成立,则实数m的最大值为( )
对一切x∈(0,1]恒成立,则实数m的最大值为( )| A.0 | B.2 | C.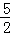 | D.3 |
B
由定义可知不等式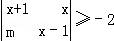 化简为(x﹣1)(x+1)﹣mx≥﹣2,
化简为(x﹣1)(x+1)﹣mx≥﹣2,
即x2﹣mx+1≥0对一切x∈(0,1]恒成立,
∴mx≤x2+1,
∵x∈(0,1],
∴m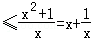 恒成立.
恒成立.
设f(x)=x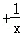 ,
,
则f'(x)=1﹣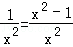 ,
,
则当x∈(0,1]时,f'(x)≤0,
∴函数f(x)单调第减,∴函数f(x)的最小值为f(1)=1+1=2,
∴m≤2,
即实数m的最大值为2.
故选:B.
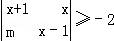 化简为(x﹣1)(x+1)﹣mx≥﹣2,
化简为(x﹣1)(x+1)﹣mx≥﹣2,即x2﹣mx+1≥0对一切x∈(0,1]恒成立,
∴mx≤x2+1,
∵x∈(0,1],
∴m
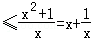 恒成立.
恒成立.设f(x)=x
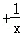 ,
,则f'(x)=1﹣
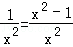 ,
,则当x∈(0,1]时,f'(x)≤0,
∴函数f(x)单调第减,∴函数f(x)的最小值为f(1)=1+1=2,
∴m≤2,
即实数m的最大值为2.
故选:B.

练习册系列答案
相关题目
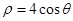 .
.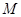 时,求函数
时,求函数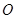 的单调增区间;
的单调增区间;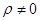 时,求函数
时,求函数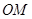 在区间
在区间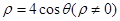 上的最小值;
上的最小值;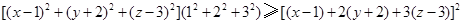 图象为曲线
图象为曲线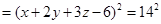 ,设点
,设点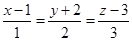 ,
,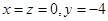 是曲线
是曲线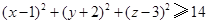 上不同的两点,点
上不同的两点,点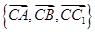 为线段
为线段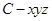 的中点,过点
的中点,过点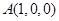 作
作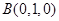 轴的垂线交曲线
轴的垂线交曲线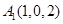 于点
于点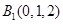 .试问:曲线
.试问:曲线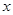 在点
在点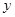 处的切线是否平行于直线
处的切线是否平行于直线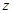 ?并说明理由.
?并说明理由.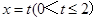 左侧的图形的面积为
左侧的图形的面积为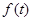 ,则
,则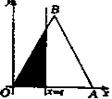
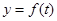 的图像在点P(t0,f(t0))处的切线的斜率为
的图像在点P(t0,f(t0))处的切线的斜率为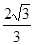 ,则t0=____________.
,则t0=____________.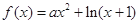 .
.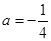 时,求函数
时,求函数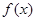 的单调区间;
的单调区间;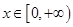 时,函数
时,函数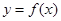 图象上的点都在
图象上的点都在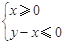 所表示的平面区域内,不等式
所表示的平面区域内,不等式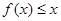 恒成立,求实数
恒成立,求实数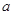 的取值范围.
的取值范围. 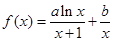 ,曲线
,曲线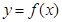 在点
在点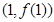 处的切线方程为
处的切线方程为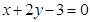 。
。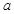 、
、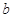 的值;
的值;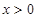 ,且
,且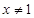 时,
时,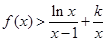 ,求
,求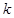 的取值范围。
的取值范围。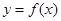 定义域内的一个子区间,若存在
定义域内的一个子区间,若存在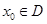 ,使
,使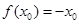 ,则称
,则称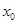 是
是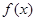 的一个“次不动点”,也称
的一个“次不动点”,也称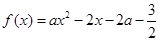 在区间
在区间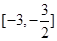 上存在次不动点,则实数a的取值范围是( )
上存在次不动点,则实数a的取值范围是( )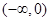
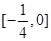
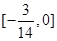

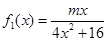 ,
,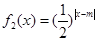 ,其中m∈R.
,其中m∈R.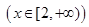 的单调性,并证明你的结论;
的单调性,并证明你的结论;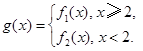 若对任意大于等于2的实数x1,总存在唯一的小于2的实数x2,使得g (x1) =" g" (x2) 成立,试确定实数m的取值范围.
若对任意大于等于2的实数x1,总存在唯一的小于2的实数x2,使得g (x1) =" g" (x2) 成立,试确定实数m的取值范围.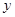 =
=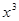
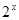 的导函数是( )
的导函数是( )