题目内容
已知α、β均为锐角,若p:sinα<sin(α+β),q:α+β<![]() ,则p是q的( )
,则p是q的( )
|
| A. | 充分而不必要条件 | B. | 必要而不充分条件 |
|
| C. | 充要条件 | D. | 既不充分也不必要条件 |
考点:
必要条件、充分条件与充要条件的判断;正弦函数的单调性.
分析:
由α、β均为锐角,我们可以判断sinα<sin(α+β)时,α+β<![]() 是否成立,然后再判断α+β<
是否成立,然后再判断α+β<![]() 时,sinα<sin(α+β)是否成立,然后根据充要条件的定义进行判断.
时,sinα<sin(α+β)是否成立,然后根据充要条件的定义进行判断.
解答:
解:当sinα<sin(α+β)时,α+β<![]() 不一定成立
不一定成立
故sinα<sin(α+β)⇒α+β<![]() ,为假命题;
,为假命题;
而若α+β<![]() ,则由正弦函数在(0,
,则由正弦函数在(0,![]() )单调递增,易得sinα<sin(α+β)成立
)单调递增,易得sinα<sin(α+β)成立
即α+β<![]() ⇒sinα<sin(α+β)为真命题
⇒sinα<sin(α+β)为真命题
故p是q的必要而不充分条件
故选B.
点评:
本题考查的知识点是充要条件的定义,即若p⇒q为假命题且q⇒p为真命题,则命题p是命题q的必要不充分条件

练习册系列答案
相关题目
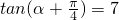 ,
, ,α,β均为锐角.
,α,β均为锐角.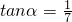 ,
,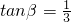 ,α,β均为锐角
,α,β均为锐角 如图,点B在以PA为直径的圆周上,点C在线段AB上,已知
如图,点B在以PA为直径的圆周上,点C在线段AB上,已知 如图,点B在以PA为直径的圆周上,点C在线段AB上,已知
如图,点B在以PA为直径的圆周上,点C在线段AB上,已知 ,设
,设 ,
, 均为锐角.
均为锐角. ;
; 的数量积
的数量积 的值.
的值.