题目内容
已知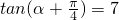
，
，α，β均为锐角．
（1）求tanα； （2）求cos（α+β）．
解：（1）tanα=tan[（α+
）-]=
=
=
．
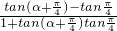（2）∵α∈（0，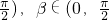
），∴sinα=
，
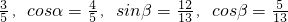cos（α+β）=cosαcosβ-sinαsinβ=-
．
分析：（1）根据tanα=tan[（α+）-]，利用两角差的正切 公式求得结果．
（2）由 α∈（0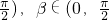，），可得sinα=，
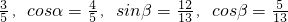由cos（α+β）=cosαcosβ-sinαsinβ 求出结果．
点评：本题考查两角和差的正切、余弦公式的应用，同角三角函数的基本关系，求出sinα和 cosα的值，是解题的关键．
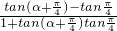）-]===．（2）∵α∈（0，
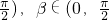），∴sinα=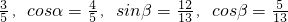，cos（α+β）=cosαcosβ-sinαsinβ=-
．分析：（1）根据tanα=tan[（α+
）-]，利用两角差的正切 公式求得结果．（2）由 α∈（0，
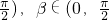），可得sinα=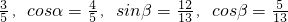，由cos（α+β）=cosαcosβ-sinαsinβ 求出结果．
点评：本题考查两角和差的正切、余弦公式的应用，同角三角函数的基本关系，求出sinα和 cosα的值，是解题的关键．
练习册系列答案
相关题目
的每条棱长均为
，
为棱
上的动点，
∥平面
，并证明之；
所成锐二面角的正切值。
