题目内容
过椭圆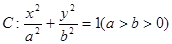 的左顶点
的左顶点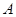 的斜率为
的斜率为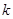 的直线交椭圆
的直线交椭圆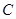 于另一个点
于另一个点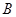 ,且点
,且点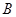 在
在 轴上的射影恰好为右焦点
轴上的射影恰好为右焦点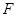 ,若
,若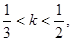 则椭圆离心率的取值范围是( )
则椭圆离心率的取值范围是( )
A.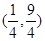 | B.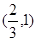 | C.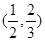 | D.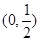 |
C
解析试题分析:因为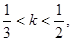 所以点
所以点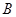 在第一象限,由题意可知点
在第一象限,由题意可知点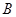 的坐标为
的坐标为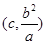 ,因为点
,因为点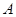 的坐标为
的坐标为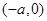 ,所以
,所以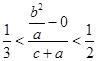 ,又因为
,又因为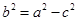 ,所以可以解得椭圆离心率的取值范围是
,所以可以解得椭圆离心率的取值范围是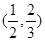 .
.
考点:本小题主要考查直线与椭圆的位置关系、顶点、焦点的应用和椭圆离心率的求解,考查学生数形结合思想的应用和运算求解能力.
点评:圆锥曲线问题一般运算量比较大,要尽量应用数形结合的数学思想,尽量使运算简单.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
下列方程的曲线关于y轴对称的是( )
| A.x2-x+y2=1 | B.x2y+xy2=1 |
| C.x2-y2=1 | D.x-y="1" |
过点(0,1)与双曲线 仅有一个公共点的直线共有 ( )
仅有一个公共点的直线共有 ( )
| A.1条 | B.2条 | C.3条 | D.4条 |
已知椭圆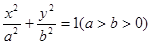 的左、右两焦点分别为
的左、右两焦点分别为 ,点
,点 在椭圆上,
在椭圆上,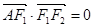 ,
,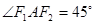 ,则椭圆的离心率
,则椭圆的离心率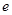 等于 ( )
等于 ( )
A. | B.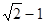 | C.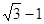 | D.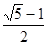 |
设椭圆的标准方程为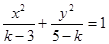 ,若其焦点在
,若其焦点在 轴上,则
轴上,则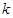 的取值范围是( )
的取值范围是( )
A.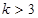 | B.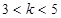 |
C.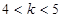 | D. |
直线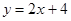 与抛物线
与抛物线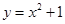 所围成封闭图形的面积是( )
所围成封闭图形的面积是( )
A.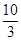 | B.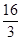 | C.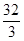 | D.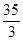 |
已知双曲线 的一条渐近线方程为
的一条渐近线方程为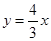 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A.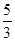 | B.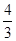 | C.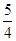 | D. |
( )抛物线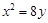 的准线方程是
的准线方程是
A.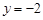 | B.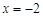 | C.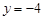 | D. |
中心在原点,焦点在y轴上,若长轴长为18,且两个焦点恰好将长轴三等分,则椭圆的方程是 ( )
A.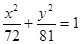 | B.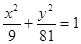 |
C.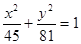 | D. |