题目内容
下表是某厂1~4月份用水量(单位:百吨)的一组数据:
由散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归直线方程是=-0.7x+a,则a等于( )
| A.10.5 | B.5.15 | C.5.2 | D.5.25 |
D
解析试题分析:因为 ,所以样本中心点为
,所以样本中心点为 。将点
。将点 代入线性回归方程可得
代入线性回归方程可得 。故D正确。
。故D正确。
考点:线性回归方程。

练习册系列答案
相关题目
某班的全体学生参加消防安全知识竞赛,成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100].若低于60分的人数是15,则该班的学生人数 ( )
| A.45 | B.50 | C.55 | D.60 |
在吸烟与患肺病这两个分类变量的计算中,下列说法正确的是( )
A.若 的观测值为 的观测值为 ,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病 ,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病 |
| B.从独立性检验可知有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患有肺病 |
| C.若从统计量中求出有95% 的把握认为吸烟与患肺病有关系,是指有5% 的可能性使得推判出现错误 |
| D.以上三种说法都不正确 |
在线性回归模型 中,下列说法正确的是( )
中,下列说法正确的是( )
A. 是一次函数 是一次函数 |
B.因变量 是由自变量 是由自变量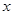 唯一确定的 唯一确定的 |
C.因变量 除了受自变量 除了受自变量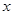 的影响外,可能还受到其它因素的影响,这些因素会导致随机误差 的影响外,可能还受到其它因素的影响,这些因素会导致随机误差 的产生 的产生 |
D.随机误差 是由于计算不准确造成的,可以通过精确计算避免随机误差 是由于计算不准确造成的,可以通过精确计算避免随机误差 的产生 的产生 |
实验测得四组(x,y)的值分别为(1,2),(2,3),(3,4),(4,4),则y与x间的线性回归方程是( )
| A.y=-1+x | B.y=1+x | C.y=1.5+0.7x | D.y=1+2x |
在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居众显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列① ~ ⑤各个选项中,一定符合上述指标的是 ( )
①平均数 ; ②标准差
; ②标准差 ; ③平均数
; ③平均数 且标准差
且标准差 ;
;
④平均数 且极差小于或等于2;⑤众数等于1且极差小于或等于4。
且极差小于或等于2;⑤众数等于1且极差小于或等于4。
| A.①② | B.③④ | C.③④⑤ | D.④⑤ |
下列说法正确的是( )
| A.样本的数据个数等于频数之和 |
| B.扇形统计图可以告诉我们各部分的数量分别是多少 |
| C.如果一组数据可以用扇形统计图表示,那么它一定可以用频数分布直方图表示 |
| D.将频数分布直方图中小长方形上面一边的一个端点顺次连结起来,就可以得到频数折线图 |
 分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样; ;
; 与
与 的随机变量K2的观测值k来说,k越小,判断“
的随机变量K2的观测值k来说,k越小,判断“