题目内容
【题目】已知各项为正数的数列![]() 满足:
满足:![]() 且
且![]() .
.
(1)证明:数列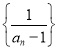 为等差数列.
为等差数列.
(2)若![]() ,证明:对一切正整数n,都有
,证明:对一切正整数n,都有![]()
【答案】(1)证明见解析.(2)证明见解析.
【解析】
(1)根据所给递推公式,将式子变形,即可由等差数列定义证明数列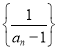 为等差数列.
为等差数列.
(2)根据数列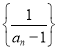 为等差数列,结合等差数列通项公式求法求得通项公式,并变形后令
为等差数列,结合等差数列通项公式求法求得通项公式,并变形后令![]() .由
.由![]() 求得
求得![]() 的取值范围,即可表示出
的取值范围,即可表示出![]() ,由不等式性质进行放缩,求得
,由不等式性质进行放缩,求得![]() 后,即可证明不等式成立.
后,即可证明不等式成立.
(1)证明:各项为正数的数列![]() 满足:
满足:![]()
则![]() ,
,![]() ,
,
同取倒数可得![]() ,
,
所以![]() ,
,
由等差数列定义可知数列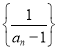 为等差数列.
为等差数列.
(2)证明: 由(1)可知数列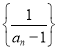 为等差数列.,
为等差数列.,
则数列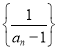 是以
是以![]() 为首项,以
为首项,以![]() 为公差的等差数列.
为公差的等差数列.
则![]() ,
,
令![]() ,
,
因为![]() ,
,
所以![]() ,
,
则![]() ,
,
所以![]() ,
,
所以![]()
![]() ,
,
所以![]()
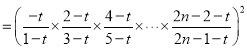
![]()
由不等式性质可知,若![]() ,则
,则![]() 总成立,
总成立,
因而![]() ,
,
所以![]()
![]()
![]()
![]()
所以![]()
不等式得证.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
【题目】某校医务室欲研究昼夜温差大小与高三患感冒人数多少之间的关系,他们统计了2019年9月至2020年1月每月8号的昼夜温差情况与高三因患感冒而就诊的人数,得到如下资料:
日期 | 2019年9月8日 | 2019年10月8日 | 2019年11月8日 | 2019年12月8日 | 2020年1月8日 |
昼夜温差 | 5 | 8 | 12 | 13 | 16 |
就诊人数 | 10 | 16 | 26 | 30 | 35 |
该医务室确定的研究方案是先从这5组数据中选取2组,用剩下的3组数据求线性回归方程,再用被选取的2组数据进行检验.假设选取的是2019年9月8日与2020年1月8日的2组数据.
(1)求就诊人数![]() 关于昼夜温差
关于昼夜温差![]() 的线性回归方程
的线性回归方程![]() (结果精确到0.01)
(结果精确到0.01)
(2)若由(1)中所求的线性回归方程得到的估计数据与所选出的检验数据的误差均不超过3人,则认为得到的线性回归方程是理想的,试问该医务室所得线性回归方程是否理想?
参考公式: ,
,![]() .
.