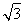Question

设函数f(x)=sin2x+

3

sinxcosx+1(x∈R)．
（Ⅰ）求函数f（x）的最小正周期及单调递增区间；
（Ⅱ）若x∈[0，

π

2

]，求函数f（x）的最大值和最小值；
（Ⅲ）若把函数f（x）的图象按向量a平移后所得函数为奇函数，求使得|a|最小的a．

Answer 1

分析：（Ⅰ）利用三角函数中的恒等变换将f（x）=sin²x+

3

sinxcosx+1化简为：f（x）=sin（2x-

π

6

）+

3

2

，利用正弦函数的性质即可求f（x）的最小正周期及单调递增区间；
（Ⅱ）利用正弦函数的单调性质可求得f（x）的最大值和最小值；
（Ⅲ）由前两问可知，2x-

π

6

=kπ时，f（x）为奇函数，从而可求得其对称中心，继而可求得|

a

|最小时对应的向量．

解答：（本小题13分）
解：∵f（x）=sin²x+

3

sinxcosx+1
=

1-cos2x

2

+

3

2

sin2x+1
=

3

2

sin2x-

1

2

cos2x+

3

2

…（2分）
（Ⅰ）函数f（x）的最小正周期
T=

2π

2

=π…（3分）
令2kπ-

π

2

≤2x-

π

6

≤2kπ+

π

2

⇒kπ-

π

6

≤x≤kπ+

π

3

，
即函数f（x）的单调递增区间为[kπ-

π

6

，kπ+

π

3

]（k∈Z）．…（5分）
（Ⅱ）∵x∈[0，

π

2

]，
∴2x-

π

6

∈[-

π

6

，

5π

6

]，
∴sin（2x-

π

6

）∈[-

1

2

，1]，
所以函数f（x）的最小值为1，最大值为

5

2

…（9分）
（Ⅲ）令2x-

π

6

=kπ，x=

kπ

2

+

π

12

（k∈Z），
即函数图象对称中心为（

kπ

2

+

π

12

，

3

2

）k=0时距原点最近，则满足条件的|

a

|=（-

π

12

，-

3

2

）…（13分）

点评：本题考查三角函数中的恒等变换，考查正弦函数的最小正周期、单调区间、最值及对称中心，熟练掌握正弦函数的性质是解决问题的基础，属于中档题．