Question

设函数f(x)=-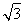sin2ωx-sinωxcosωx(ω>0),且y=f(x)图象的一个对称中心到最近的对称轴的距离为.

(1)求ω的值;

(2)求f(x)在区间[π,]上的最大值和最小值.

 

Answer 1

【答案】

(1) ω=1 (2) ,-1

【解析】

解:(1)f(x)=-sin2ωx-sinωxcosωx

=-·-sin2ωx

=cos2ωx-sin2ωx

=-sin(2ωx-).

因为图象的一个对称中心到最近的对称轴的距离为,

又ω>0,

所以=4×,

因此ω=1.

(2)由(1)知f(x)=-sin(2x-).

当π≤x≤时,≤2x-≤.

所以-≤sin(2x-)≤1.

因此-1≤f(x)≤.

故f(x)在区间[π,]上的最大值和最小值分别为,-1.