题目内容
【题目】在平面直角坐标系xOy中,直线l的参数方程为  (t为参数).以O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程为ρ=2acosθ(a>0),且曲线C与直线l有且仅有一个公共点.
(t为参数).以O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程为ρ=2acosθ(a>0),且曲线C与直线l有且仅有一个公共点.
(Ⅰ)求a;
(Ⅱ)设A、B为曲线C上的两点,且∠AOB= ![]() ,求|OA|+|OB|的最大值.
,求|OA|+|OB|的最大值.
【答案】解:(Ⅰ)∵直线l的参数方程为  (t为参数),
(t为参数),
∴直线l的普通方程是x+ ![]() ﹣3=0,
﹣3=0,
∵曲线C的极坐标方程为ρ=2acosθ(a>0),
∴曲线C的直角坐标方程是(x﹣a)2+y2=a2,
依题意直线l与圆相切,则d= ![]() =a,
=a,
解得a=﹣3,或a=1,
∵a>0,∴a=1.
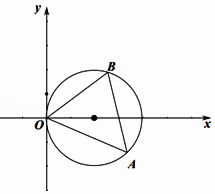
(Ⅱ)如图,不妨设A(ρ1,θ),B(ρ2, ![]() ),
),
则ρ1=2cosθ, ![]() ,
,
|OA|+|OB|=ρ1+ρ2=2cosθ+2cos( ![]() )=3cosθ﹣
)=3cosθ﹣ ![]() =2
=2 ![]() cos(
cos( ![]() ),
),
∴θ+ ![]() =2kπ,即
=2kπ,即 ![]() ,k∈Z时,|OA|+|OB|最大值是2
,k∈Z时,|OA|+|OB|最大值是2 ![]() .
.
【解析】(Ⅰ)直线l的参数方程消去参数,能求出直线l的普通方程;由曲线C的极坐标方程能求出曲线C的直角坐标方程,依题意直线l与圆相切,由此能求出a的值.(Ⅱ)设A(ρ1,θ),B(ρ2, ![]() ),则|OA|+|OB|=ρ1+ρ2=2cosθ+2cos(
),则|OA|+|OB|=ρ1+ρ2=2cosθ+2cos( ![]() )=3cosθ﹣
)=3cosθ﹣ ![]() =2
=2 ![]() cos(
cos( ![]() ),由此能求出|OA|+|OB|的最大值.
),由此能求出|OA|+|OB|的最大值.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案
相关题目


