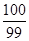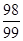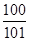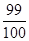题目内容
(本题满分12分)
已知数列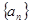 的通项公式为
的通项公式为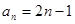 ,数列
,数列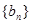 的前n项和为
的前n项和为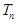 ,且满足
,且满足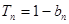
(I)求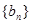 的通项公式;
的通项公式;
(II)在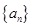 中是否存在使得
中是否存在使得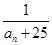 是
是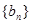 中的项,若存在,请写出满足题意的一项(不要求写出所有的项);若不存在,请说明理由.
中的项,若存在,请写出满足题意的一项(不要求写出所有的项);若不存在,请说明理由.
已知数列
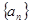 的通项公式为
的通项公式为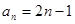 ,数列
,数列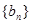 的前n项和为
的前n项和为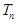 ,且满足
,且满足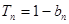
(I)求
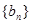 的通项公式;
的通项公式;(II)在
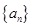 中是否存在使得
中是否存在使得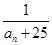 是
是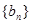 中的项,若存在,请写出满足题意的一项(不要求写出所有的项);若不存在,请说明理由.
中的项,若存在,请写出满足题意的一项(不要求写出所有的项);若不存在,请说明理由.(I)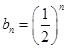 (II)
(II)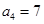
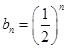 (II)
(II)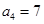
试题分析:(I)当
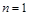 时,
时,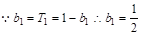 ………………………………………2分
………………………………………2分当
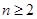 时,
时,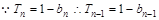
两式相减得:
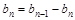 ,即:
,即: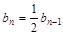 …………………………………………6分
…………………………………………6分故{
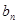 }为首项和公比均为
}为首项和公比均为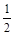 的等比数列,
的等比数列,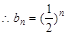 ……………………………8分
……………………………8分(II)设
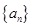 中第m项
中第m项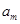 满足题意,即
满足题意,即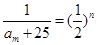 ,即
,即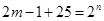
所以
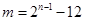 (
(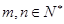 )比如:
)比如: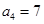 ……………………12分
……………………12分点评:数列
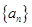 由前n项和
由前n项和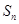 求通项
求通项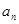 时需分
时需分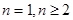 两种情况
两种情况 ,最后验证两种情况下的结果能否合并到一起
,最后验证两种情况下的结果能否合并到一起
练习册系列答案
相关题目
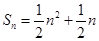
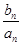 ,求数列
,求数列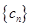 的通项公式
的通项公式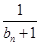 +
+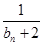 +…+
+…+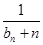 >
>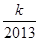 对任意正整数n均成立?若存在,求出k的最大值,若不存在,说明理由.
对任意正整数n均成立?若存在,求出k的最大值,若不存在,说明理由.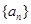 的前
的前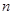 项和为
项和为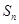 ,且有
,且有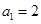 ,
,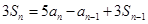
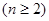 .
.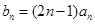 ,求数列
,求数列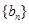 的前
的前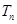 ;
;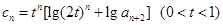 ,且数列
,且数列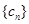 中的 每一项总小于它后面的项,求实数
中的 每一项总小于它后面的项,求实数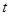 的取值范围.
的取值范围.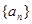 的前n项和为
的前n项和为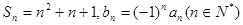 ,则数列
,则数列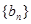 的前50项的和为( )
的前50项的和为( )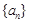 的前
的前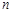 项和为
项和为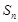 ,且
,且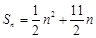 。数列
。数列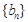 满足
满足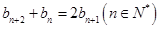 ,
,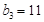 ,
,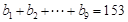 。
。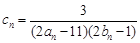 ,数列
,数列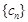 的前
的前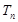 ,求使不等式
,求使不等式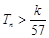 对一切
对一切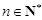 都成立的最大正整数
都成立的最大正整数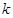 的值;
的值;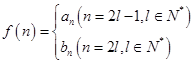 ,是否存在
,是否存在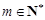 ,使得
,使得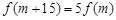 成立?若存在,求出
成立?若存在,求出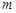 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。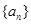 中,
中,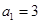 ,
,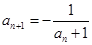 (
(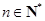 ),能使
),能使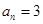 的
的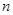 可以等于( ).
可以等于( ).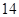
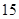
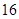
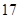
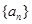 是等比数列,公比
是等比数列,公比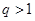 ,前
,前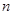 项和为
项和为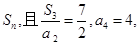
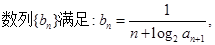
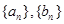 的通项公式;
的通项公式;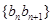 的前
的前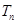 ,求证
,求证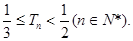
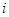 行第
行第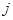 列的数为
列的数为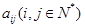 ,则:
,则: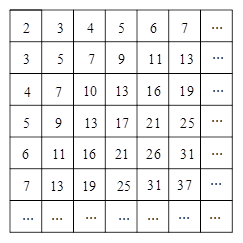
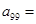 ; (Ⅱ)表中数
; (Ⅱ)表中数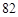 共出现 次.
共出现 次.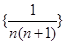 的前
的前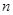 项和为
项和为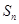 ,则
,则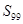 等于
等于