题目内容
若a,b,c均为实数,且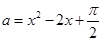 ,
,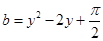 ,
,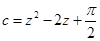 ,
,
试用反证法证明:a,b,c中至少有一个大于0.
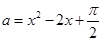 ,
,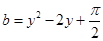 ,
,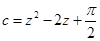 ,
,试用反证法证明:a,b,c中至少有一个大于0.
见解析.
利用反证法证明时,先否定结论,然后利用否定后的结论,结合已知的公理或者定理产生矛盾,说明假设不成立,原命题成立。设a、b、c都不大于0,a≤0,b≤0,c≤0,∴a+b+c≤0,而a+b+c=(x2-2y+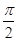 )+(y2-2z+
)+(y2-2z+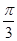 )+(z2-2x+
)+(z2-2x+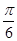 )
)
∴a+b+c>0,这与a+b+c≤0矛盾。
(反证法)证明:设a、b、c都不大于0,a≤0,b≤0,c≤0,∴a+b+c≤0,
而a+b+c=(x2-2y+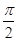 )+(y2-2z+
)+(y2-2z+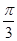 )+(z2-2x+
)+(z2-2x+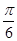 )
)
=(x2-2x)+(y2-2y)+(z2-2z)+π=(x-1)2+(y-1)2+(z-1)2+π-3,
∴a+b+c>0,这与a+b+c≤0矛盾,故a、b、c中至少有一个大于0.
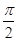 )+(y2-2z+
)+(y2-2z+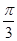 )+(z2-2x+
)+(z2-2x+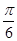 )
)∴a+b+c>0,这与a+b+c≤0矛盾。
(反证法)证明:设a、b、c都不大于0,a≤0,b≤0,c≤0,∴a+b+c≤0,
而a+b+c=(x2-2y+
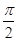 )+(y2-2z+
)+(y2-2z+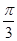 )+(z2-2x+
)+(z2-2x+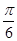 )
)=(x2-2x)+(y2-2y)+(z2-2z)+π=(x-1)2+(y-1)2+(z-1)2+π-3,
∴a+b+c>0,这与a+b+c≤0矛盾,故a、b、c中至少有一个大于0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
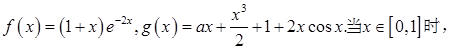

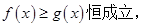
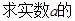 取值范围.
取值范围. , 求证:
, 求证: .
.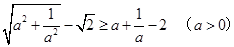
 ,
, 满足
满足 ,求证:
,求证:


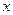 是正实数,求证:
是正实数,求证: ;
;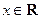 ,不等式
,不等式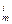 <miA
<miA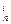

 且
且 ,
, 为大于1的自然数,
为大于1的自然数,