题目内容
已知函数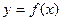 是
是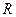 上的奇函数,当
上的奇函数,当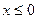 时,
时,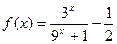 ,
,
(1)判断并证明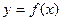 在
在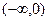 上的单调性;
上的单调性;
(2)求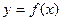 的值域;
的值域;
(3)求不等式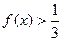 的解集。
的解集。
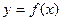 是
是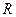 上的奇函数,当
上的奇函数,当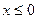 时,
时,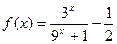 ,
,(1)判断并证明
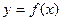 在
在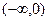 上的单调性;
上的单调性;(2)求
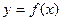 的值域;
的值域; (3)求不等式
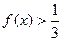 的解集。
的解集。解:(1)设 ,则
,则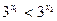 ,
,
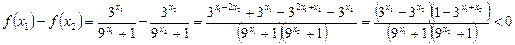 ,
,
∴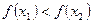 ,即
,即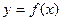 在
在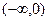 上是增函数。
上是增函数。
(2)∵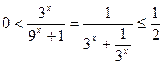 ,∴当
,∴当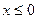 时,
时,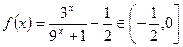 ;
;
∵当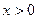 时,
时,
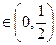 。
。
综上得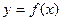 的值域为
的值域为 。
。
(3)∵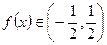 ,又∵
,又∵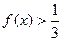 ,∴
,∴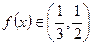 ,
,
此时 单调递增,∵
单调递增,∵ ,
,
∴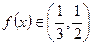 时,
时, 。令
。令 ,
,
即 ,
,
∴不等式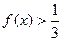 的解集是
的解集是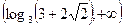
 ,则
,则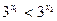 ,
,
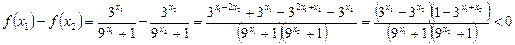 ,
,∴
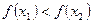 ,即
,即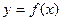 在
在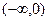 上是增函数。
上是增函数。(2)∵
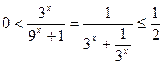 ,∴当
,∴当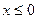 时,
时,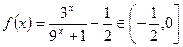 ;
;∵当
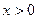 时,
时,
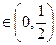 。
。综上得
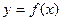 的值域为
的值域为 。
。(3)∵
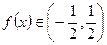 ,又∵
,又∵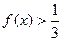 ,∴
,∴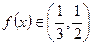 ,
,此时
 单调递增,∵
单调递增,∵ ,
,∴
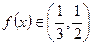 时,
时, 。令
。令 ,
,即
 ,
,∴不等式
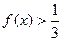 的解集是
的解集是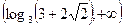
略

练习册系列答案
相关题目




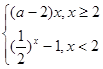 是R上的单调减函数,则实数a的取值
是R上的单调减函数,则实数a的取值 ]
]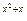 ≤(
≤(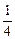 )x-2,求函数y=2x-2-x的值域.
)x-2,求函数y=2x-2-x的值域. 的单调递增区间为
的单调递增区间为 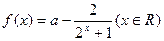
 ,求实数
,求实数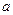 的值;
的值;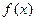 的值域
的值域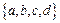 的子集个数有16个
的子集个数有16个 ;②定义在
;②定义在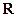 上的奇函数
上的奇函数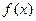 必满足
必满足 ;③
;③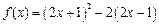 既不是奇函数又不是偶函数;④偶函数的图像一定与
既不是奇函数又不是偶函数;④偶函数的图像一定与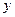 轴相
轴相 交;⑤
交;⑤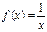 在
在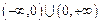 上是减函数。其中真命题的序号是 (把你认为正确的命题的序号都填上).
上是减函数。其中真命题的序号是 (把你认为正确的命题的序号都填上). 上定义在R上的奇函数,且当
上定义在R上的奇函数,且当 时,
时, ,若
,若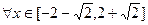 ,不等式
,不等式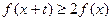 恒成立,则实数
恒成立,则实数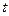 的取值范围是
的取值范围是 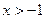 时,函数
时,函数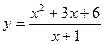 的最小值为__________________。
的最小值为__________________。