题目内容
已知矩阵A=[
],α=[
],且Aα=[
].
(1)求实数x,y的值;
(2)求A的特征值λ1,λ2(λ1>λ2)及对应的特征向量
,
;
(3)计算A20α.
|
|
|
(1)求实数x,y的值;
(2)求A的特征值λ1,λ2(λ1>λ2)及对应的特征向量
| α1 |
| α2 |
(3)计算A20α.
(1)∵A=[
],α=[
],Aα=[
],
∴Aα=[
][
]=[
]=[
],解得:
,
∴实数x,y的值分别为3,4;
(2)矩阵A的特征多项式为矩阵M的特征多项式为f(λ)=λ2-7λ+6,
令f(λ)=0,得矩阵M的特征值为6或1,
当λ=6时由二元一次方程
得x-y=0,令x=1,则y=1,
所以特征值λ=6对应的特征向量为
=
,
当λ=1时由二元一次方程
得2x+3y=0,
令x=3,则y=-2,
所以特征值λ=1对应的特征向量为
=
;
(3)令[
]=m
+n
,
∴
,解得:
,
故A20α=620
+120
=
.
|
|
|
∴Aα=[
|
|
|
|
|
∴实数x,y的值分别为3,4;
(2)矩阵A的特征多项式为矩阵M的特征多项式为f(λ)=λ2-7λ+6,
令f(λ)=0,得矩阵M的特征值为6或1,
当λ=6时由二元一次方程
|
所以特征值λ=6对应的特征向量为
| α1 |
|
当λ=1时由二元一次方程
|
令x=3,则y=-2,
所以特征值λ=1对应的特征向量为
| α2 |
|
(3)令[
|
|
|
∴
|
|
故A20α=620
| α1 |
| α2 |
|

练习册系列答案
相关题目
 所做的前两题计分。作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将选题号填入括号中
所做的前两题计分。作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将选题号填入括号中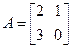 的特征值及对应的特征向量。
的特征值及对应的特征向量。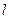 的参数方程:
的参数方程: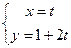 (
(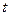 为参数)和圆
为参数)和圆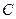 的极坐标方程:
的极坐标方程: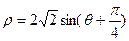 。
。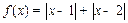 . 若不等式
. 若不等式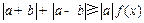
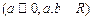 恒成立,求实数
恒成立,求实数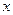 的范围。
的范围。 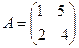 ,求A的特征值以及属于每个特征值的一个特征向量。
,求A的特征值以及属于每个特征值的一个特征向量。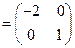 的特征值和特征向量.
的特征值和特征向量.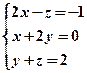 的增广矩阵是__________________.
的增广矩阵是__________________.