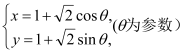题目内容
【题目】已知数列![]() 满足:
满足:![]() ,
,![]() .
.
(1)求最小的正实数![]() ,使得对任意的
,使得对任意的![]() ,恒有
,恒有![]() ;
;
(2)求证:对任意的正整数![]() ,恒有
,恒有![]() .
.
【答案】(1)1;(2)证明见解析.
【解析】
试题分析:(1)已知条件是数列的递推式,比较复杂,在证明时,可先计算数列的前几项,如![]() .想象即归纳出结论数列
.想象即归纳出结论数列![]() 是递减数列,从而
是递减数列,从而![]() 的最小值为1,因此只要证明
的最小值为1,因此只要证明![]() ,可用数学归纳法证(2)
,可用数学归纳法证(2)
证明;(2)由(1)可得数列![]() 是单调递减的正项数列.,这样右边的证明较方便,只要重新放缩可得,
是单调递减的正项数列.,这样右边的证明较方便,只要重新放缩可得,
![]() ,从而
,从而![]() ,左边不等式的证明较难,左边先放缩为
,左边不等式的证明较难,左边先放缩为![]() ,从而
,从而![]() ,左右同除
,左右同除![]() 得:
得:![]() ,即
,即![]() ,利用累加法求
,利用累加法求![]() (其中求和
(其中求和![]() ,可用裂项相消或错位相减法求得),可证明不等式.
,可用裂项相消或错位相减法求得),可证明不等式.
试题解析:(1)由于![]() ,
,![]() ,
,![]() ,
,
由此我们可以猜想![]() 为单调递减数列,因此我们猜测
为单调递减数列,因此我们猜测![]() 的最小值为1,下面我们证明
的最小值为1,下面我们证明![]() .
.
![]() ,故当
,故当![]() 时,数列
时,数列![]() 为单调递减数列,从而
为单调递减数列,从而![]() .
.
![]() ,由于
,由于![]() ,且当
,且当![]() 时,有
时,有![]()
从而对任意的![]() ,恒有
,恒有![]() ,又由于
,又由于![]() ,从而所求的最小正实数
,从而所求的最小正实数![]() .
.
(说明:若用数学归纳法证明,也同样给满分)
事实上,由于![]() ,假设
,假设![]() 时,
时,![]() ,则当
,则当![]() 时,
时,
考虑到![]() ,从而
,从而![]() ,
,![]() .
.
从而![]() ,
,
从而由数学归纳法原理得:对任意的![]() ,恒有
,恒有![]() .
.
又由于![]() ,从而所求的最小正实数
,从而所求的最小正实数![]() .
.
(2)由于![]() ,则
,则![]() ,
,
从而数列![]() 是单调递减的正项数列.
是单调递减的正项数列.
一方面,![]() ,从而
,从而![]()
另一方面,![]() ,从而
,从而![]() ,
,
左右同除![]() 得:
得:![]() ,即
,即![]()
设
![]() (也可利用错位相减法求解
(也可利用错位相减法求解 ,两式相减得
,两式相减得
![]() ,从而
,从而
![]() )
)
从而由![]() ,得,
,得,
当![]() 时,
时,![]()
从而![]() ,即
,即 ,
,
即当![]() 时,
时,![]() ,又当
,又当![]() 时,
时,![]() ,从而对任意的
,从而对任意的![]() ,恒有
,恒有![]() .
.
综上所示,对任意的正整数![]() ,恒有
,恒有![]() .
.

练习册系列答案
相关题目