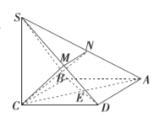
题目内容
【题目】已知![]() ,
,![]() 为两非零有理数列(即对任意的
为两非零有理数列(即对任意的![]() ,
,![]() ,
,![]() 均为有理数),
均为有理数),![]() 为一个无理数列(即对任意的
为一个无理数列(即对任意的![]() ,
,![]() 为无理数).
为无理数).
(1)已知![]() ,并且
,并且![]() 对任意的
对任意的![]() 恒成立,试求
恒成立,试求![]() 的通项公式;
的通项公式;
(2)若![]() 为有理数列,试证明:对任意的
为有理数列,试证明:对任意的![]() ,
,![]() 恒成立的充要条件为
恒成立的充要条件为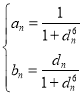 ;
;
(3)已知![]() ,
,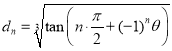 ,试计算
,试计算![]() .
.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】
(1)根据不等式可得![]() ,把
,把![]() 代入即可解出
代入即可解出![]()
(2)根据![]() 化简,利用
化简,利用![]() 为有理数即可解决
为有理数即可解决
(3)根据题意可知,本题需分![]() 为奇数和偶数时讨论,通过
为奇数和偶数时讨论,通过![]() 求出
求出![]() .
.
(1)∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
(2)∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() 为有理数列,
为有理数列,![]() 为无理数列,
为无理数列,
∴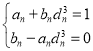 ,∴
,∴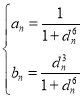 ,以上每一步可逆.
,以上每一步可逆.
(3)![]() ,∴
,∴![]() .
.
∵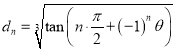 ,∴
,∴![]() ,
,
当![]() 时,∴
时,∴![]()
当![]() 时,∴
时,∴![]() ,∴
,∴![]() 为有理数列,
为有理数列,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() 为有理数列,
为有理数列,![]() 为无理数列,
为无理数列,
∴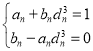 ,∴
,∴![]() ,
,
∴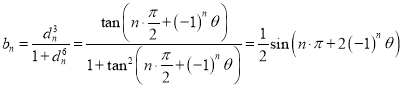
当![]() 时,∴
时,∴![]()
当![]() 时,∴
时,∴![]() ,
,
∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】自由购是一种通过自助结算购物的形式.某大型超市为调查顾客自由购的使用情况,随机抽取了100人,调查结果整理如下:
20以下 | [20,30) | [30,40) | [40,50) | [50,60) | [60,70] | 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(1)现随机抽取1名顾客,试估计该顾客年龄在[30,50)且未使用自由购的概率;
(2)从被抽取的年龄在[50,70]使用的自由购顾客中,随机抽取2人进一步了解情况,求这2人年龄都在[50,60)的概率;
(3)为鼓励顾客使用自由购,该超市拟对使用自由购顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋?