题目内容
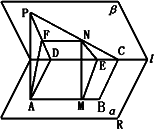
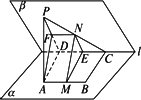
如图，在二面角M-l-N的一个M内有Rt△ABC，其中∠A=90°，顶点B、C在二面角的棱l上，AB、AC与平面N所成的角分别为α、β，若二面角M-l-N的大小为θ，则下面的关系式中正确的是（ ）分析：作AD⊥l于点D，作AE⊥平面N于点E，连结BE、CE、DE．证出∠ADE是二面角M-l-N的平面角，∠ABE、∠ACE分别为AB、AC与平面N所成的角，得∠ADE=θ、∠ABE=α且∠ACE=β．设AE=x，利用解三角形算出AB=
、AC=
且AD=
，在Rt△ABC中利用勾股定理与等积转换得到
=
+
，代入前面的数据化简整理即可得到
sin2α+sin2β=sin2θ，从而选出正确答案．
| x |
| sinα |
| x |
| sinβ |
| x |
| sinθ |
| 1 |
| AD2 |
| 1 |
| AB2 |
| 1 |
| AC2 |
sin2α+sin2β=sin2θ，从而选出正确答案．
解答：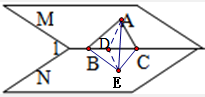
解：作AD⊥l于点D，作AE⊥平面N于点E，连结BE、CE、DE
∵AE⊥平面N，∴DE是AD在平面N内的射影
∵AD⊥l，∴DE⊥l，
可得∠ADE就是二面角M-l-N的平面角，∠ADE=θ
又∵BE、CE分别是AB、AC在平面N的射影
∴∠ABE、∠ACE分别为AB、AC与平面N所成的角，得∠ABE=α且∠ACE=β
设AE=x，则Rt△ABE中，sinα=
，可得AB=
=
同理得到AC=
，AD=
∵Rt△ABC中，AD为斜边BC边上的高
∴AD=
，得
=
=
+
，
因此
=
+
，化简得sin2α+sin2β=sin2θ
故选：B
解：作AD⊥l于点D，作AE⊥平面N于点E，连结BE、CE、DE∵AE⊥平面N，∴DE是AD在平面N内的射影
∵AD⊥l，∴DE⊥l，
可得∠ADE就是二面角M-l-N的平面角，∠ADE=θ
又∵BE、CE分别是AB、AC在平面N的射影
∴∠ABE、∠ACE分别为AB、AC与平面N所成的角，得∠ABE=α且∠ACE=β
设AE=x，则Rt△ABE中，sinα=
| AE |
| AB |
| AE |
| sinα |
| x |
| sinα |
同理得到AC=
| x |
| sinβ |
| x |
| sinθ |
∵Rt△ABC中，AD为斜边BC边上的高
∴AD=
| AB•AC |
| BC |
| 1 |
| AD2 |
| AB2+AC2 |
| AB2•AC2 |
| 1 |
| AB2 |
| 1 |
| AC2 |
因此
| sin2θ |
| x2 |
| sin2α |
| x2 |
| sin2β |
| x2 |
故选：B
点评：本题给出锐二面角，在一个半平面内有Rt△ABC，直角边AB、AC与另一个半平面所成角已知的情况下，探索这两个角与二面角大小之间的关系．着重考查了二面角的平面角的定义及求法、直线与平面所成角和解直角三角形等知识，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
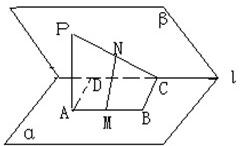如图：在二面角α-l-β中，A、B∈α，C、D∈l，ABCD为矩形，p∈β，PA⊥α，且PA=AD，M、N依次是AB、PC的中点，
