题目内容
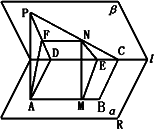
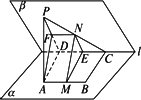
如图，在二面角M-l-N中，直角三角形ABC在面M内，斜边AB在棱l上，两直角边AC、BC与面N所成的角分别为α、β，二面角M-l-N的大小为θ.
求证：sin2α＋sin2β＝sin2θ.
证明：作CC′⊥平面N于点C′，作C′D⊥l于点D，连结CD，则CD⊥l，
∴∠CDC′是二面角MlN的平面角，∠CDC′＝θ.
又∠CAC′＝α，∠CBC′＝β，在△ABC中，CD⊥AB,∠ACB＝90°，
∴CD·AB＝AC·BC.
∴
＝
＝
＝
+
.在△CC′D中，设CC′＝a，
由∠CC′D＝90°，∠CDC′＝θ，CD＝
，
得
＝
.
在△CC′A和△CC′B中，同样可得
=
，
＝
，因此
＝
＋
，即sin2α＋sin2β＝sin2θ．
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
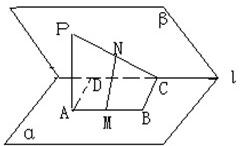如图：在二面角α-l-β中，A、B∈α，C、D∈l，ABCD为矩形，p∈β，PA⊥α，且PA=AD，M、N依次是AB、PC的中点，
如图，在二面角M-l-N的一个M内有Rt△ABC，其中∠A=90°，顶点B、C在二面角的棱l上，AB、AC与平面N所成的角分别为α、β，若二面角M-l-N的大小为θ，则下面的关系式中正确的是（ ）
