题目内容
数列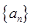 的前
的前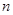 项和记为
项和记为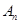 ,
,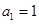 ,
,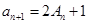 (
(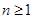 ) (Ⅰ)求
) (Ⅰ)求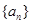 的通项公式;
的通项公式;
(Ⅱ)等差数列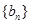 的各项为正,其前
的各项为正,其前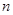 项和为
项和为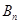 ,且
,且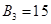 ,又
,又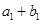 ,
,
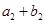 ,
,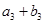 成等比数列,求
成等比数列,求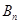 的表达式;
的表达式;
(3)若数列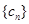 中
中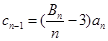 (
(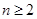 ),求数列
),求数列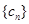 的前
的前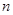 项和
项和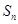 的
的
表达式.
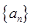 的前
的前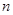 项和记为
项和记为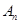 ,
,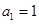 ,
,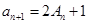 (
(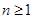 ) (Ⅰ)求
) (Ⅰ)求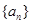 的通项公式;
的通项公式;(Ⅱ)等差数列
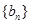 的各项为正,其前
的各项为正,其前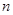 项和为
项和为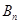 ,且
,且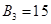 ,又
,又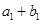 ,
,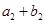 ,
,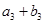 成等比数列,求
成等比数列,求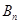 的表达式;
的表达式;(3)若数列
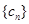 中
中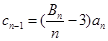 (
(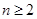 ),求数列
),求数列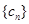 的前
的前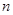 项和
项和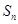 的
的表达式.
(Ⅰ) 由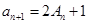 可得
可得  (
(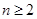 ),
),
两式相减得 ,于是
,于是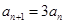 (
(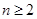 ),
),
又 ∴
∴  ,
,
故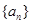 是首项为
是首项为 ,公比为
,公比为 得等比数列, ∴
得等比数列, ∴  ………………4分
………………4分
(Ⅱ)设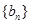 的公差为
的公差为 , 由
, 由 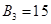 ,可得
,可得 ,得
,得 ,
,
故可设 ,
, 又
又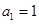 ,
, ,
, ,
,
由题意可得 , 解得
, 解得  ,
, ,
,
∵等差数列 的各项为正,∴
的各项为正,∴ ,于是
,于是 ,
,
 ; ……………………………8分
; ……………………………8分
(3) (
(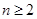 ),
), (
(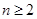 ),
), (
(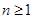 ),
),
 1
1
于是, 2
2
两式相减得:
 .
.
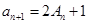 可得
可得  (
(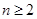 ),
),两式相减得
 ,于是
,于是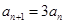 (
(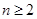 ),
),又
 ∴
∴  ,
,故
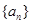 是首项为
是首项为 ,公比为
,公比为 得等比数列, ∴
得等比数列, ∴  ………………4分
………………4分(Ⅱ)设
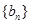 的公差为
的公差为 , 由
, 由 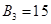 ,可得
,可得 ,得
,得 ,
,故可设
 ,
, 又
又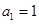 ,
, ,
, ,
,由题意可得
 , 解得
, 解得  ,
, ,
,∵等差数列
 的各项为正,∴
的各项为正,∴ ,于是
,于是 ,
, ; ……………………………8分
; ……………………………8分(3)
 (
(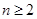 ),
), (
(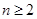 ),
), (
(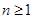 ),
), 1
1于是,
 2
2两式相减得:

 .
. 略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,
中, ,
, 是其前
是其前 项和,且
项和,且 .
.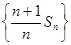 是等差数列;
是等差数列; ,记数列
,记数列 的前
的前 .
. 时,
时,

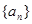 的前n项和为Sn=2n2,
的前n项和为Sn=2n2,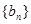 为等比数列,且
为等比数列,且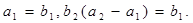
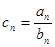 ,求数列
,求数列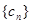 的前n项和Tn.
的前n项和Tn. 前
前 项和
项和 ,则
,则



 满足
满足 ,则数列
,则数列 _______________.
_______________.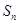 为等差数列
为等差数列 的前
的前 项和,若
项和,若 ,公差
,公差 ,
, ,则
,则  ________
________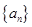 的前
的前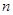 项和为
项和为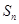 ,若
,若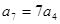 ,则
,则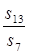 =
=  给定数列
给定数列 ,
,

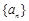 是公比为
是公比为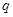 的等比数列,且
的等比数列,且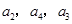 成等差数列,则
成等差数列,则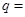 _______
_______